(1) 待ち時間が0になるまでに要する時間 ( モデル的ケースにおいて )
-
【 問 題 】
-
ある鍼灸院の実質治療時間は 8時 から 12時 までで、1人の鍼灸師が仕事をしています。鍼灸師の患者1人あたりの治療時間は常に 10分間 です。鍼灸師は患者が途切れない限り途中休憩を取りません。治療開始時刻までに6人の患者が来院し、治療開始と同時に1人の患者が来院し、その後 11:45 まで 15分毎 に定期的に患者が1人ずつ来院しました。患者の来院順に治療をするとして、鍼灸師が初めて途中休憩できるのは何時何分ですか?
便宜上、患者の入れ替わりは瞬時に行われ、先着待ち患者がない場合は、患者の来院と同時に治療が始まるものとします。
-
鍼灸師が1時間あたりに診療する患者数は、6人 です。
治療開始後1時間あたりに来院する患者数は、4人 です。
治療開始時刻までに来院した患者6人を全て治療するのに 6×1/6 時間 かかります。その間にたまる新たな待ち患者数は 6×1/6÷1/4 人 です。彼らを全て治療するのに 6×1/6÷1/4×1/6 時間 かかります。その間にたまる新たな待ち患者数は 6×1/6÷1/4×1/6÷1/4 人 です。彼らを全て治療するのに 6×1/6÷1/4×1/6÷1/4×1/6 時間 かかります。その間にたまる新たな待ち患者数は 6×1/6÷1/4×1/6÷1/4×1/6÷1/4 人 です。このようにしてn回繰り返すと、n回目は、彼らを全て治療するのに 6/4×(4/6)n 時間 かかります。その間にたまる新たな待ち患者数は 6×(4/6)n 人です。そして、それぞれの合計は次のように収束します。
治療時間の合計: 3時間
治療した患者数の合計: 6+12 =→ 18人
なぜなら、
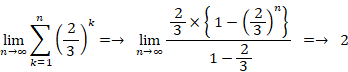
したがって、8時 から 11時 までの3時間で18人の患者を治療すると、11時以降は患者の待ち時間が0になります。したがって、鍼灸師が初めて途中休憩できるのは、11:10 になります。その後は、5分間休んで10分間治療してを3回繰り返して、11:55 に治療が終わります。
-
8時 から 9時 の間6人の治療が終わり、9:05 には 5人が治療を持っている状態になる。9時 から 10時 の間6人の診療が終わり、10:05 には3人が治療を持っている状態になる。その3人は 9:30 と 9:45 と 10:00 に来院した患者である。10時 から 111時 の間6人の診療が終わる。10:30 に来院した患者は 10:40 からの治療となり、10:45 に来院した患者は 10:50 からの治療となる。そして、11時以降は治療待ち患者がなくなり患者の待ち時間が0になる。したがって、鍼灸師が初めて途中休憩できるのは、11:10 になる。
-
たとえばマッサージ店のように、生産と販売と購入と消費が同時に行われるようなサービス商品を提供している店において、サービス提供が開始されるまでの待ち時間について考えてみましょう。考えやすくするため、マッサージ師は1人であるとし、そのマッサージ師は客がいないときのみ休憩を取るものとします。その店では、マッサージ師がサービスを提供する時間は客1人あたり常に 20分間 です。店内には常時客が3人います。現在サービスを受けている客が1人とサービスを待っている客が2人です。というのも、店の外では行列ができているのですが、店内が3蜜にならないよう、会計が終わって客が出てきたらそれと入れ替えに店内ヘと誘導するシステムになっているからです。便宜上、会計は瞬時に終わるものとしてください。



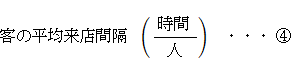
② = 1/① ④ = 1/③
需要と供給のバランスが釣り合っているとき( 店内に限ってのことだけど常時3人である ):
② = ④ = 1/3 ( 時間 / 人)
① = ③ = 3 ( 人 / 時間 )
-
新たな客が店に入った時刻において、1番目の店内待ち客の待ち時間は 20分間 であり、2番目の店内待ち客の待ち時間は 40分間 であり、2人の平均待ち時間は 30分間 になります。また、無作為の時刻に何度も調査される1番目の店内待ち客の平均待ち時間は 10分間 であり、2番目の店内待ち客の平均待ち時間は 30分間で あり、2人の平均待ち時間の平均値は 20分間 になります。
-
【 問 題 】
-
あるクリ/ニックでは1人の医師が仕事をしています。医師の患者1人あたりの診療時間は平均 6人/時間 の指数分布に従います。医師は患者が途切れない限り途中休憩を取りません。診察開始と同時に2人の患者が来院し、その後患者が来院しますが、それは、平均 4人/時間 ごとの指数分布に従います。患者の平均待ち時間は何分間になりますか?
便宜上、患者の入れ替わりは瞬時に行われ、先着待ち患者がない場合は、患者の来院と同時に診療が始まるものとします。
-
仕事効率は 4/6 =→ 2/3 になります。
もし、医師が患者が途切れない限り途中休憩を取らずに永遠に働き続けるのであれば、答えは、次の公式より導かれます。


=→ 20 分間
この問題は統計学の高度な問題です。この公式の根拠は、今の私には分かりません。
診察患者数が増えるに従って待ち時間が 20分間 に近づくのが分かります。
プログラムの内容 :
 その他の数学 へ戻る
その他の数学 へ戻る