三角形の重心が原点にあるとき、 三角形のそれぞれの頂点の位置ベクトルの内積行列は三角形の辺の長さを用いて表すことができます。

　 三角形ＡＢＣの辺ＡＢの長さを x 、 辺ＡＣの長さを y 、 辺ＢＣの長さを z とします。 三角形ＡＢＣの重心が直交座標系の原点に重なるように置き、 Ａの位置ベクトルを 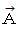，Ｂの位置ベクトルを 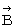， Ｃの位置ベクトルを 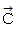とします。 すると、 ３つのベクトルたちの内積行列 は次のようになります。

　　　　　
　　　　　

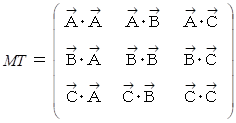
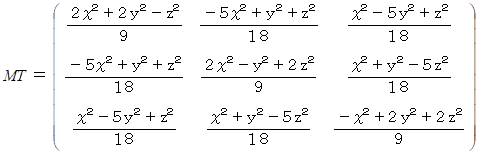
　 なぜこのような式で表されるのかを、 今回は考えてみることにしましょう。

三角形の頂点 Ａ, Ｂ,Ｃ の相互の間隔 （ 辺の長さたち ） を表す行列を次のように表すことにします。
　　　　　

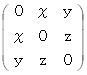
行列の要素をすべて２乗してから２で割ると次のようになります。
　　　　　

第１行目、 ２行目、 ３行目 の平均値をそれぞれ m₁ ， m₂ ， m₃　とすると、
　　　　　

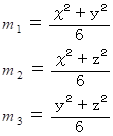
すべての要素の平均を m₀　とすると、
　　　　　

そこで、 次のような行列を作ります。
　　　

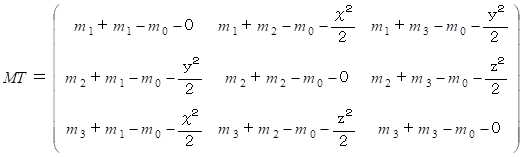
これを x，y，z で表すと次のようになります。

　　　

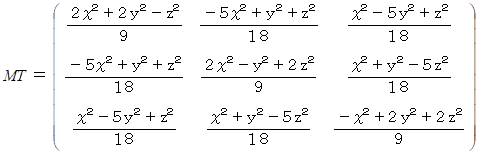
なぜなら、 たとえば、 第１行第２列 の要素を計算すると次のようになるので。

　　　　　

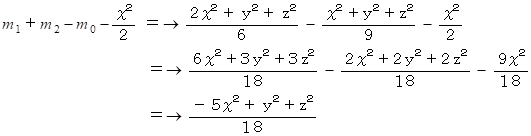
　 Ａの位置座標を 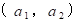、 Ｂの位置座標を 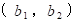とすると、 Ｃの位置座標は 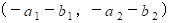になります。 　 これから、 行列 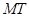を a₁ ， a₂， b₁， b₂　を用いて表すようにしていきます。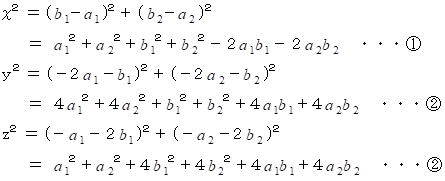

　　　　　

　　　
　　　
　　　
　　　
　　　
　　　

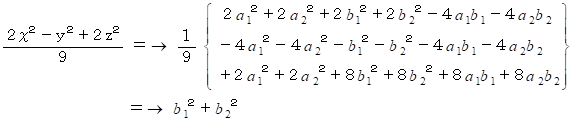
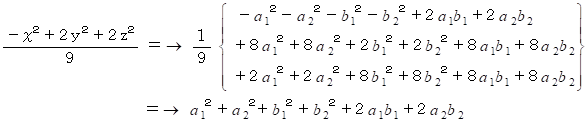
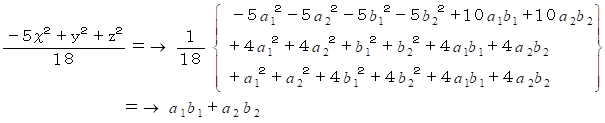
したがって、
　　　
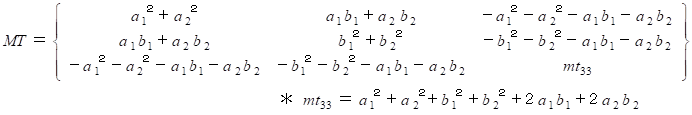
ここで、
　　　　　

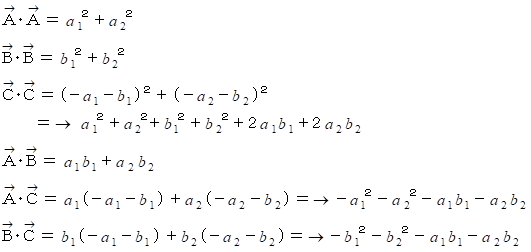
したがって、
　　　

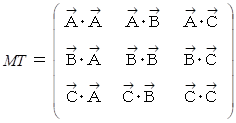
ちなみに、
　　　

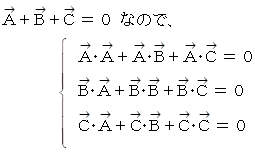
　※ 参照： 大学生のための数学 ＞ 統計学 ＞ 多次元尺度構成法 ( MDS )