多次元尺度構成法 ( MDS ) とは、２点間のそれぞれの距離や親近度のデータを、図に点として見やすく配置する方法である。たとえば、４つの点があり、それらの相互の距離がわかっているときに、４つの点の重心からの距離と４つの点の重心からの位置ベクトルが相互になす角度を導き出せば、４つの点の位置関係を図に描くことができる。

距離行列 : Ａ
　　点 P₁ , P₂ , P₃ , P₄ がある。
　　
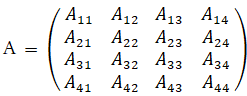
　　　　　　　　　　※　A_gr ： 点 P_g から 点 P_r への距離
　　　　　　　　　　　　　　　g ＝ 1, 2, 3, 4　　r ＝ 1, 2, 3, 4

行列Ａを加工して行列Ｂを作る：
　　
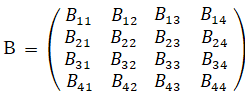
　　　　　　　　　　※　B_gr ＝ A_gr² / 2
　　　　　　　　　　　　　　(例)　B₁₂ ＝ A₁₂² / 2

m_g ＝ ( B_g1 ＋ B_g2 ＋ B_g3 ＋ B_g4 ) / 4
　　　(例)　m₁ ＝ ( B₁₁ ＋ B₁₂ ＋ B₁₃ ＋ B₁₄ ) / 4
m₀ ＝ ( m₁ ＋ m₂ ＋ m₃ ＋ m₄ ) / 4

行列Ｂを加工して行列Ｃを作る：
　　
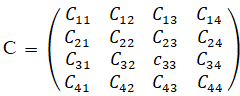
　　　　　　　　　　※　C_gr ＝ m_g ＋ m_r − m₀ − B_gr
　　　　　　　　　　　　　　(例)　C₁₂ ＝ m₁ ＋ m₂ − m₀ − B₁₂
　　　　　　　　　　　　　　　　　C₂₁ ＝ m₂ ＋ m₁ − m₀ − B₂₁

C は内積行列になっている。内積行列とは、次のようなものである。
　　　


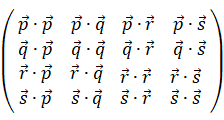
【 例 題 】

　平面上に４点 P₁ , P₂ , P₃ , P₄ があり、それら相互の距離は次のようになっている。
４点の位置関係を図示せよ。
　　　点 P₁ と P₂ との距離： 10
　　　点 P₁ と P₃ との距離： 12
　　　点 P₁ と P₄ との距離： 10
　　　点 P₂ と P₃ との距離： 10
　　　点 P₂ と P₄ との距離： 16
　　　点 P₃ と P₄ との距離： 10

【 解 答 】

　　　　　　　

　　　　　　　


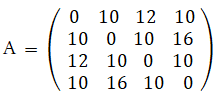
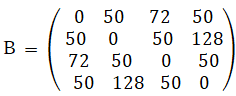
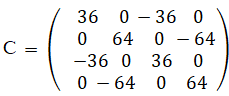
この内積行列から言えること：
　　　点 P₁ と P₃ の位置ベクトルの大きさは 6 である。
　　　点 P₂ と P₄ の位置ベクトルの大きさは 8 である。
　　　点 P₁ と P₂ および P₄ の位置ベクトルは直交する。
　　　点 P₂ と P₃ の位置ベクトルは直交する。
　　　点 P₃ と P₄ の位置ベクトルは直交する。

したがって、４点を図示すると、次のようになる。

　　
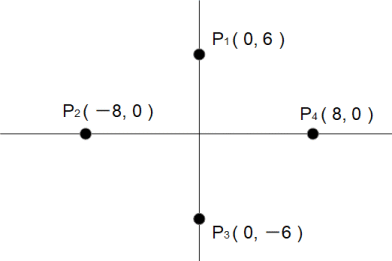
　　　　　　　　※　点 P₂ と 点 P₄ を座標系の横軸上に取った。

　※ 参考：　その他の数学 ＞ 重心が原点にある三角形の内積行列
　※ 参考：　その他の数学 ＞ 方向類似度 と 相性度 のイメージ