（１） 方向類似度

　 全体集合を、 始点と存在平面を共有する大きさ １ のベクトルとします。
２つのベクトルの方向がどれくらい似ているのかを表すのに、 次の２つの指標を用いることにします。

　　　　　

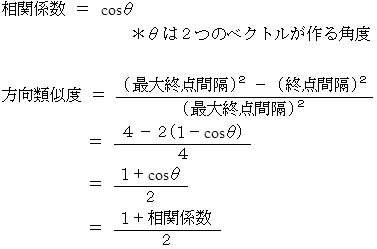
相関係数 のとりうる範囲は −１ 〜 １ です。
方向類似度 のとりうる範囲は ０ 〜 １ です。
方向類似度 は、 言うなれば、 相関係数を ０ 〜 １ の範囲になるように修正したものです。
相関係数については、 統計学 ＞ 相関関係の解析　をご覧ください。

（２） 相性度 と 距離感

　 さて、「 ２人一発じゃんけん対決５番勝負 」は「 自己対決 」というのがあって、 その場合、 鏡の中の自分と対決することになります。 ５回のうちで勝敗のつかなかった回数（ あいこだった回数 ）を ｎ とします。 そして次のような指標を作ります。
　　　　　

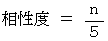
相性度 は、 方向類似度 に相当します。 したがって、 次の式が成り立ちます。
　　　　　

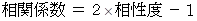
次に、 距離感 を次のように定義します。
　　　　　

さて、 ４人に協力してもらって実験したところ、 それぞれの相性度 は次のような結果になりました。


	Ａさん	Ｂさん	Ｃさん	Ｄさん
Ａさん	１		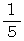０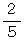
Ｂさん		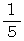１		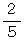０
Ｃさん	０		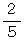１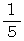
Ｄさん		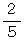０		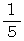１


相性度の行列 ：
　　　　　

相関係数の行列 ：
　　　　　

距離感の行列 ：
　　　　　

各要素を２乗してから２で割ります。
　　　　　

さらに、 次のようの操作をして行列Ｓ を作ります。

　　　　　

　　　　　

　　　　　

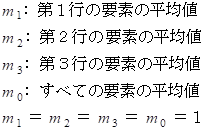
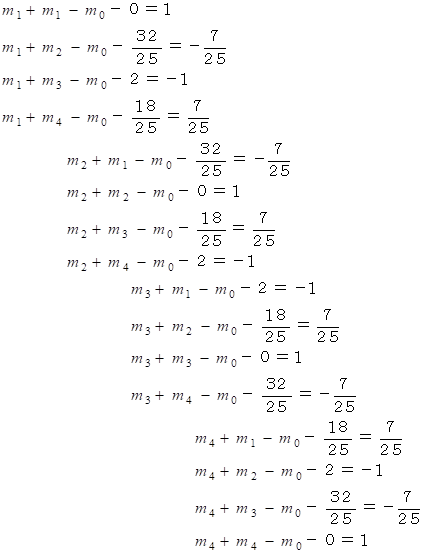
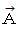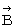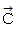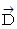， ， ， を それぞれ 点 Ａ， Ｂ， Ｃ， Ｄ の位置ベクトルとすると、
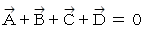のとき、 原点は４つの点を結んで作られる平面図形の重心に位置します。
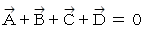のとき、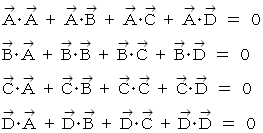
　　　　　

　　　　　このときの 内積行列 を Ｔ とすると、
　　　　　　　　　

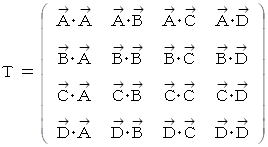
　　　　　行列Ｓ と 行列Ｔ は同じものであるので、 次の式たちが成り立ちます。
　　　　　　　　　

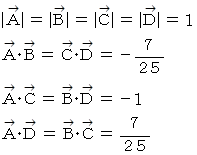
　　　　　したがって、
　　　　　　　　　
　　　　　　　　　
　　　　　　　　　
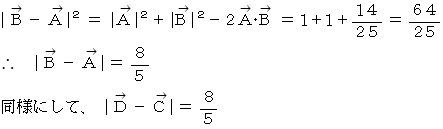
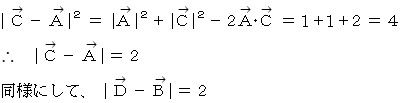
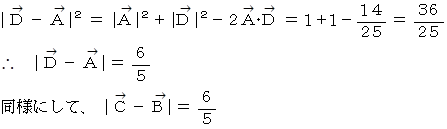
　　　　　以上、 距離感 がきちんと保たれていることが解りました。

　　　　　また、
　　　　　　　　　


以上から、 ４つの点の位置関係は次のような平面図で表すことができます。

　　　　　　

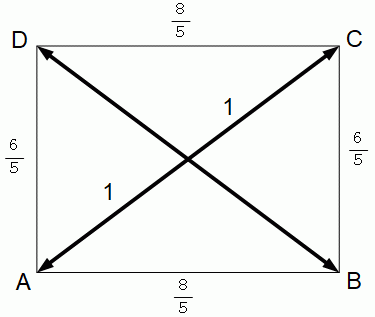
　 ４つの点 Ａ， Ｂ， Ｃ， Ｄ は、 それぞれの相性度を距離で表すときのＡさんの位置、 Ｂさんの位置、Ｃさんの位置、 Ｄさんの位置を表しています。 こういう手法は、 多次元尺度構成法 で用いられます。

　※ 参考：　統計学 ＞ 多次元尺度構成法 ( MDS )