例題５ ：
-
「
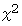が奇数であるならば、 
は奇数である。」ということを証明してください。-
この包含命題の前提命題 ：
「
は、 ２乗すると奇数になる数で構成される集合の要素である。」この包含命題の結論命題 ：
「
は、奇数の集合の要素である。」この包含命題の対偶 ：
「
が偶数ならば、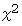 
は偶数である。」これから、 対偶が真の包含命題であることを証明します。
は偶数なので、 次のように表すことができます。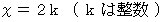
すると、
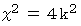となり、 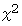が偶数であることがわかります。 したがって、 この包含命題の対偶は真であることがわかりました。 したがって、 この包含命題は真であることがわかります。-
「
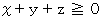ならば、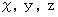 
のうち少なくとも１つは０以上の数である。」 ということを証明してください。-
この包含命題の前提命題 ：
「
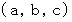は、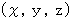 
のそれぞれに代入すると 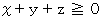を満たす３つの数の順列で構成される集合の要素である。」
この包含命題の結論命題 ：
「
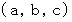は、 少なくとも１つは０以上になっている３つの数の順列で構成される集合の要素である。」
この包含命題の対偶 ：
「
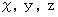のすべてが０未満ならば、 
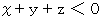である。」 です。この対偶の前提命題 ：
「
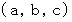は、 ３つの０未満の数の順列で構成される集合の要素である。」この対偶の結論命題 ：
「
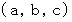は、 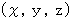のそれぞれに代入すると 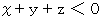を満たす３つの数の順列で構成される集合の要素である。」
３つの０未満の数の順列で構成される集合は、
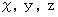に代入すると 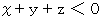を満たす３つの数の順列で構成される集合に属していることは明白です。 つまり、 前提命題の要素は結論命題の要素でもあることは明白です。 したがって、 この対偶が真であることがわかりました。 したがって、 この包含命題は真であることがわかります。
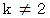ならば、 次の連立１次方程式を解くことができることを証明してください。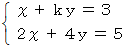
-
この包含命題の前提命題 ：
「
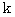は２以外の数で構成される集合の要素である。」この包含命題の結論命題 ：
「
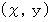のそれぞれに数を代入したときに、 次の連立１次方程式を満たす２つの数の順列で構成される集合は空集合ではない。
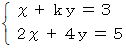」この包含命題の対偶の前提命題 ：
「
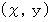のそれぞれに数を代入したときに、 次の連立１次方程式を満たす２つの数の順列で構成される集合は空集合である。
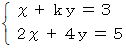」この包含命題の対偶の結論命題 ：
「
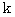は２のみの数で構成される集合の要素である。」この包含命題の対偶が真であることを証明します。
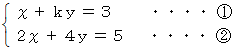
の両辺に 
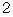をかけたものと 
の両辺に 
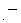
をかけたものと を辺々加えます。 すると次のようになります。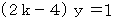
上の式において、
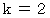のときのみ、 異なる数をイコールで結ぶことになり矛盾が生じます。 また、 それ以外の時は、 次のようになり矛盾が生じません。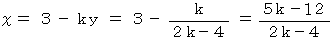
以上のことより、
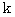が２以外のときは連立方程式の解があり、 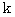が２のときは連立方程式の解がないことがわかります。 したがって、 この包含命題の対偶の前提命題の対象集合の要素のすべては、 ２ になります。 また、 この包含命題の対偶の結論命題の対象集合の要素のすべては、 ２ になります。 したがって、 この対偶が真であることがわかりました。 よって、 この包含命題は真であることがわかります。例題８ ：
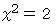を満足する はすべて無理数であることを証明してください。-
この命題は、 次のように書き換えることができます。
「
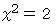が を満足するならば、 は無理数である。」この包含命題の前提命題 ：
「
は、 に代入すると 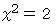を満足する数で構成される集合の要素である。」この包含命題の結論命題 ：
「
は無理数の集合の要素である。」この包含命題の結論命題の否定 ：
「
は有理数の集合の要素である。」まず、「
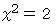は無理数の集合の要素ではない。」 と仮定します。 つまり、「 が を満足するならば、 は有理数である。」 という命題が真であると仮定します。すると、 次のように表されます。
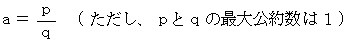
これを
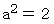に代入すると、 次のようになります。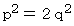
この式より、
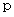は偶数であることがわかります。 したがって、 次のように置きます。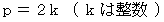
すると、次のようになります。
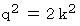
この式より、
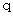は偶数であることがわかります。すると、 最初の定義
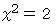に矛盾します。 したがって、 最初の仮定が間違っていたことになります。 したがって、 は無理数であることがわかりました。 つまり、 に代入すると を満足する数はすべて無理数であることがわかりました。
論文の最初 へ戻る