「 包含命題 」の「 前件 」が真であるとして論理を進めていき、「 包含命題 」の「 後件 」が真であることを明らかにするのが 集合論的証明法 です。「 前件 」が真であり、 かつ、「 後件 」が真であるときは、 その「 包含命題 」は「 真 」になります。 証明のための集合論であることを意識化するために、「 包含命題 」の「 前件 」を「 前提命題 」と言い、「 包含命題 」の「 後件 」を「 結論命題 」と言うことにします。

　 集合論的証明法の基本その１ は、「 命題Ａ は真である。 よって、 命題Ｂ は真である。」という論法によって、「 命題Ｂ は真である。」ということを導くことです。 このとき、 命題Ａ の対象集合 が 命題Ｂ の対象集合 の部分集合になっていることを、 明示するか暗黙の了解にしておかなければなりません。 命題Ａ の対象集合 が 命題Ｂ の対象集合 の部分集合であるとき、 すなわち、 命題Ａ の対象集合 が 命題Ｂ の対象集合に含まれるとき、「 命題Ｂ は偽である。 よって、 命題Ａ は偽である。」という論法もあります。

　「 命題Ａ は真である。」の基本型は、「 は集合Ａ の要素である。」ということです。
　「 命題Ｂ は真である。」の基本型は、「 は集合Ｂ の要素である。」ということです。
　 命題Ｃ が「 否定命題 」のときは、「 命題Ｃ は真である。」とは「 は集合Ｃ の要素ではない。」ということになります。
　 集合Ａ が 集合Ｂ に含まれるとき、 すなわち、 集合Ａ が 集合Ｂ の部分集合であるとき、「 は集合Ａ の要素である。 よって、 は集合Ｂ の要素である。」と言い切ることができます。 またそのときに、「 は集合Ｂ の要素ではない。 よって、 は集合Ａ の要素ではない。」と言い切ることもできます。


　 集合論的証明法の基本その２ は、「 命題Ａ が真であるならば、 命題Ｂ は真である。」という「 包含命題 」が真であることを、 明らかにすることです。 このとき、 命題Ａ が「 前提命題 」で、 命題Ｂ が「 結論命題 」です。 包含命題が真であることを明らかにするためには、 前提命題の対象集合 が 結論命題の対象集合 の部分集合になっていることを示せばいいのですが、 そのためのには、 次のような方法があります。
　　　　前提命題の対象集合の要素たち と 結論命題の対象集合の要素たち をすべて明
　　　　　らかにする。
　　　　包含命令の対偶が真の包含命題であることを明らかにする。 対遇が真なら元の
　　　　　命題も真です。 この方法は「 対偶証明法 」と言われます。
　　　　前提命題の対象集合 が 結論命題の対象集合の補集合 の部分集合になっている
　　　　　と仮定して、 演繹的に論理を進めて矛盾を導き出し、 仮定が間違っていたと結論づ
　　　　　ける。 この手法を用いる証明法は「 背理法 」と言われます。


これから、 集合論的証明法の基本その１ の例題を２つ示します。

例題１ ：

　猫は哺乳類です。 このことから、 猫は動物であることを証明してください。

解答 ：

　哺乳類の集合は、 動物の集合に含まれます。
　猫は哺乳類の要素です。
　よって、 猫は動物の要素です。
　この証明方法は「 三段論法 」と言われます。

例題２ ：

　桜は動物ではありません。 このことから、 桜は哺乳類ではないことを証明してください。

解答 ：

　哺乳類の集合は、 動物の集合に含まれます。
　桜は動物の要素ではありません。
　よって、 桜は哺乳類の要素ではありません。
　この証明方法のことを、 私は「 対偶三段論法 」と言っています。

これから、 集合論的証明法の基本その２ の例題を１つ示します。

例題３ ：

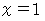　 ならば 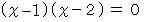であることを、 集合論を用いて証明してください。

解答 ：

この包含命題の前提命題 ：
　　　「 は、 に代入すると 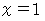を満足する数で構成される集合の要素である。」
この包含命題の結論命題 ：
　　　「 は、 に代入すると 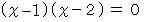を満足する数で構成される集合の要素である。」

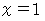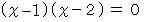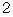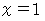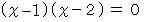　 に代入すると を満足する数で構成される集合の要素のすべては です。 に代入すると を満足する数で構成される集合の要素のすべては、 と です。 したがって、 に代入すると を満足する数で構成される集合は、 に代入すると を満足する数で構成される集合に含まれます。 は に代入すると 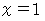を満足する数で構成される集合の要素です。 したがって、 は に代入すると 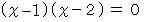を満足する数で構成される集合の要素です。 よって、 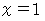ならば 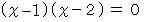になります。

これから対偶証明法を、 例題４ から 例題７ に示します。

例題４ ：

　現在の日本の婚姻法において、 「 20歳以上の人について言うと、ある人が女性と結婚する権利を持っているならば、その人はＸＹ遺伝子を持っている。」
ということを証明してください。

解答：

この包含命題の前提命題 ：
　　　「 ある人は、 女性と結婚する権利を持っている人たちの集合の要素である。」
この包含命題の結論命題 ：
　　　「 ある人は、 ＸＹ遺伝子を持っている人たちの集合の要素である。」
この包含命題の対偶 ：
　　　「 ある人がＸＸ遺伝子を持っているならば、 その人は女性と結婚する権利を持っていな
　　　い。」

　 この対偶は明らかに真です。 したがって、 女性と結婚する権利を持っている人たちの集合は、 ＸＹ遺伝子を持っている人たちの集合に含まれることがわかりました。 したがって、 この包含命題は真であることがわかりました。