（１） 線分上の点から線分上の点への写像

　長さが１の線分を構成する点の集合 から 長さが２の線分を構成する点の集合 への写像を考えます。

　　　　

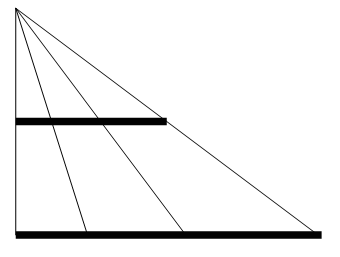
　上図より、長さが１の線分を構成する点の集合 から 長さが２の線分を構成する点の集合 への写像は１対１対応になっていることが分かります。ですから、２つの集合は同等であり、濃度も等しいことがわかります。ということは、後者の集合の隣どうしの要素の間隔は前者の２倍になっているけど、空間も２倍に拡大していると言うことができます。

（２） 面上の点から線分上の点への写像

　面積が１の正方形の辺を含まない内部の面を構成する点の集合 から その正方形の一辺を構成する点の集合 への写像を考えます。

　　　

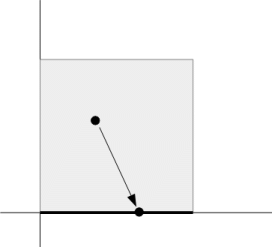
　正方形内の点 P から x 軸上の辺上のの点 P' への写像を、点が存在する場所の座標を用いて次のように表すことにします。
　　　P ( P_x, P_y )　→　P'( Q )
　　　ただし、
　　　　　P_x　＝　P_x1×10⁻¹ ＋ P_x2×10⁻² ＋ P_x3×10⁻³ ＋ P_x4×10⁻⁴ ＋ P_x5×10⁻⁵ ・・・
　　　　　P_y　＝　P_y1×10⁻¹ ＋ P_y2×10⁻² ＋ P_y3×10⁻³ ＋ P_y4×10⁻⁴ ＋ P_y5×10⁻⁵ ・・・
　　　　　Q　＝　P_x1×10⁻¹ ＋ P_y1×10⁻² ＋ P_x2×10⁻³ ＋ P_y2×10⁻⁴ ＋ P_x3×10⁻⁵ ＋ P_y3×10⁻⁶ ＋ ・・・

　すると、正方形の辺を含まない内部の面を構成する点の集合 から その正方形の一辺を構成する点の集合 への写像は１対１対応になっていることが分かります。ですから、２つの集合は同等であり、濃度も等しいことがわかります。ということは、後者の集合の隣どうしの要素の間隔は前者の x 分の１ になっているけど、空間も x 分の１ に収縮していると言うことができます。

　※ 参照： ばいおりんの日常的物理学文集 ＞ 数学と物理学 ＞ 微小２点間距離