無限に広がる平面に無限に伸びる一本の直線を引けば、平面は直線によって２つの領域に分割されます。ではｎ本の直線によって平面はいくつの領域に分割されるでしょうか？ ただし、どの直線も平行でなく、どの３本の直線も一点で交わらないものとします。

　ｎ本目に引いた直線は他のｎ−１本の直線によってｎ−２本の線分と２本の半直線に分割され、それらは１つずつ分割領域の数を増やします。したがって、ｎ本の直線が分割する平面の領域の数を a_n とすると、次の漸化式が成り立ちます。
　　　 a₁ ＝ 2
　　　 ｎ ≧ 2 のとき
　　　　　　 a_n ＝ a_n−1 ＋ ｎ

　　　 a₂ ＝ 2 ＋ 2
　　　 a₃ ＝ ( 2 ＋ 2 ) ＋ 3　＝→　2 ＋ ( 2 ＋ 3 )
　　　 a₄ ＝ 2 ＋ ( 2 ＋ 3 ) ＋ 4　＝→　2 ＋ ( 2 ＋ 3 + 4 )
　　　 a₅ ＝ 2 ＋ ( 2 ＋ 3 ＋ 4 ) + 5　＝→　2 ＋ ( 2 ＋ 3 + 4 ＋ 5 )

　　　 a_n ＝ 2 ＋ ( 2 ＋ 3 + 4 ＋ 5 ＋ ・・・ ＋ ｎ )

　　したがって、
　　　
　 　　　

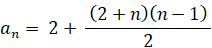
　　　　２　　４　　７　　11　　16　　22　・・・・
階差数列： ２　　３　　４　　 ５　　６　・・・