１ 〜 ５ の５枚のトランプカードを用意してください。 まず １ のカードの短い方の辺が机の端に重なるようにして置きます。 次に２のカードの ８分の１ が机上からはみ出すようにして １ のカードの上にずらして重ねます。 その次に同様にして３のカードを２のカードに対して ６分の１ ずらして重ねます。 そのまた次に４のカードを３のカードに対して ４分の１ ずらして重ねます。 最後に５のカードを４のカードに対して ２分の１ ずらして重ねます。 転倒しそうになりますがきちんとやればバランスを保ちます。 このとき５のカードは完全に机上でない空間に存在します。 驚異のバランスです。 すべてのカードを同じ割合でずらしてもこんなことはできません。

　　　　　　　

　 この積み上げ方は、土台になるカードよりも上になるカードたちの全体の重心が土台になるカードの端になるように積み上げる方法です。本当にそうなっているかどうか、上から順にみていきましょう。

　 まず、 土台の４のカードに対する５のカードです。 これは自明ですね。
　 次に、 土台の３のカードに対する４と５のカードです。 ４と５のカードの全体の重心は４のカードの端から ４分の１ の位置です。４のカードは３のカードに対して ４分の１ ずれています。 したがって、 ４と５のカードの全体の重心は土台の３のカードのちょうど端になっています。
　 その次に、 土台の２のカードに対する３と４と５のカードです。 ３と４と５のカードの全体の重心は、 ４と５のカードの全体の重心と３のカードの重心とのトルク （ トルクは回転軸からの距離と力の積で表される ） のつり合いより求められます。 ３のカード上の３と４と５のカードの全体の重心から４と５のカードの全体の重心が存在する端までの距離を １ とすると、 ３のカード上の３と４と５のカードの全体の重心から３のカードの重心が存在する中央までの距離は２になっています。 したがって、 ３と４と５のカードの全体の重心は３のカードの端から ６分の１ の位置になっています。 ３のカードは２のカードに対して ６分の１ ずれています。 したがって、 ３と４と５のカードの全体の重心は土台の２のカードのちょうど端になっています。

　 その次に、 土台の １ のカードに対する２と３と４と５のカードです。 ２と３と４と５のカードの全体の重心は、 ３と４と５のカードの全体の重心と２のカードの重心とのトルク （ トルクは回転軸からの距離と力の積で表される ） のつり合いより求められます。 ２のカード上の２と３と４と５のカードの全体の重心から３と４と５のカードの全体の重心が存在する端までの距離を １ とすると、 ２のカード上の２と３と４と５のカードの全体の重心から２のカードの重心が存在する中央までの距離は３になっています。 したがって、 ２と３と４と５のカードの全体の重心は２のカードの端から ８分の１ の位置になっています。 ２のカードは １ のカードに対して ８分の１ ずれています。 したがって、 ２と３と４と５のカードの全体の重心は土台の １ のカードのちょうど端になっています。

　 そういうわけで、 重心は必ずカードの外側には存在しないことになるので、 転倒することなく驚異のバランスが保てるのです。
　　　　
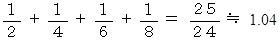
上の式より、 ５のカードは完全に机からはみ出していることが解ります。

　 同様のことを 13枚 のトランプカードで行うとどうなるでしょうか？　同様のことを 13枚 のトランプカードで行うということは、 ２のカードは １ のカードに対して 24分の１ ずらして重ねることになります。 そして、 ＫのカードはＱのカードに対して ２分の１ ずらして重ねることになります。 図で言うと、上に上にトランプを積んでいくのではなくて、一番下へ下へとトランプを入れ込んでいくのです。
　　　　
上の式より、 Ｋのカードは完全に机からカードの縦の長さの半分以上はみ出していることが解ります。

　 この原理を私は 「 持ち送りの原理 」 と言っています。 これは、 薄板を重ねて家の軒を作る時などに応用できそうですね。

　 次の式から、カードを持ち送りの原理で無数に積み上げると無限に伸びていくことが分かります。
　　　　
　　　　　　　　　　　　　　　　

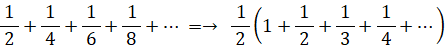
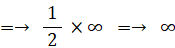
　　　　　　　　　　　※ 参照： 数理論 ＞ 平方数の数列の和（ バーゼル問題を含む ）の（２）
　 　　　　　　　　　　　　　　ばいおりんの日常的物理学文集 ＞ 錯覚と物理学 ＞ 歪転倒