(1) その1
-
多人数でジャンケンをするとき、 あいこになる確率を x とします。 x はジャンケンをする人数によって決まります。
興味のある方は JavaScript_シミュレーション > 多人数一発勝負ジャンケン をご覧ください。
何回目で初めて敗者が出現するかどうかの確率分布は次のようになります。
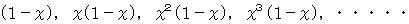
したがって、 次の式が成り立ちます。
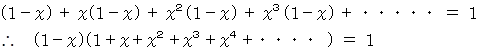
確かに、 次の式が成り立ちます。
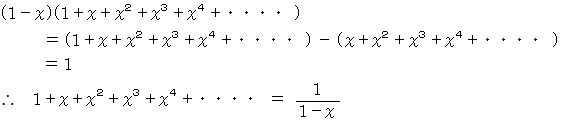
上記の式はマクローリン展開でも求めることができます。 ここで注意が必要です。 マクローリン展開できるものは x の取れる値に制限があるものが多く、 この例では −1 < x ≦ 1 の範囲でしか成立しないのです。
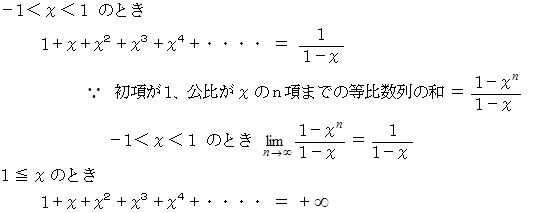
x ≦ −1 のとき、
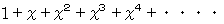 は、 収束せず、 発散せず、 振動します。
は、 収束せず、 発散せず、 振動します。-
マクローリン展開より次の式が成り立ちます。
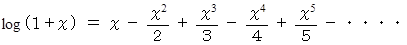
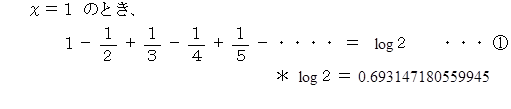
参照: 解析学 > 交代調和級数の証明
 は成立します。 次の十進BASIC のプログラムを実施すると、 そのことがわかります。
は成立します。 次の十進BASIC のプログラムを実施すると、 そのことがわかります。INPUT PROMPT "(-1↑) and (1↓)?":x
LET Q = 0
FOR i=1 TO 2000
LET Q = Q - (x^i/i)*(-1)^i
PRINT Q
NEXT i
PRINT LOG(1+x)
END
 より、 次の式たちが成り立ちます。
より、 次の式たちが成り立ちます。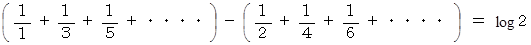
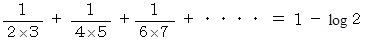
マクローリン展開より次の式が成り立ちます。
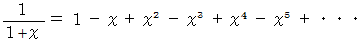
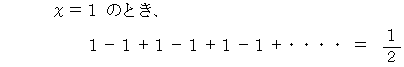
(4) その4
マクローリン展開より次の式が成り立ちます。
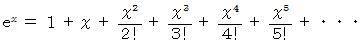
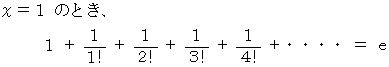
 解析学 へ戻る
解析学 へ戻る