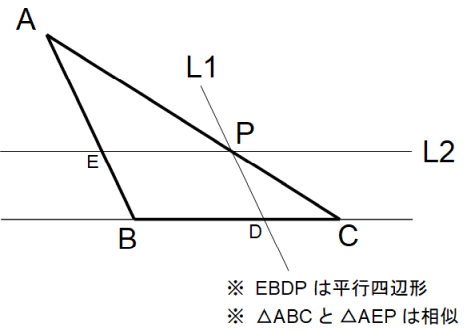
三角形ＡＢＣがあります。辺ＡＣを m：n の比に内分する点Ｐがあります。
点Ｐを通り辺ＡＢに平行な直線 L1 を引き、それが辺ＢＣと交わる点をＤとします。
点Ｐを通り辺ＢＣに平行な直線 L2 を引き、それが辺ＡＢと交わる点をＥとします。
すると、四角形ＥＢＤＰは平行四辺形になり、三角形ＡＢＣと三角形ＡＥＰは相似になります。

ＢＤ ＝ ＥＰ　　・・・ �@
ＥＢ ＝ ＡＢ−ＡＥ　　・・・ �A
ＡＥ：ＡＢ ＝ m ： m＋n　　・・・ �B
ＥＰ：ＢＣ ＝ m ： m＋n　　・・・ �C

�@ を �C に代入して、 ＢＤ：ＢＣ　＝　m ： m＋n　　・・・ �D
�A を �B に代入して、 (ＡＢ−ＥＢ) ：ＡＢ　＝ m ： m＋n
よって、 １ − ＥＢ / ＡＢ　＝　m / m＋n
よって、 ＥＢ / ＡＢ　＝　n / m＋n
よって、 ＥＢ：ＡＢ　＝　n ： m＋n　　・・・ �E

�D と �E が言いたいことです。