どの角も 180°未満の四角形について考えます。
三角形は必ず内接円と外接円とを持ちますが、 四角形はそうではありません。

　　　　　　　　角の二等分線の交点　　　　　　　　　　　　　　　　　垂直二等分線の交点
　　　　　　　　　　　　　

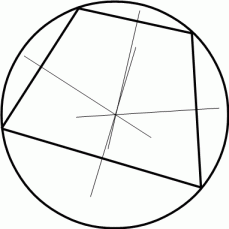
　　　　　　　Ａｅ　＝　Ａｈ
　　　　　　　Ｂｅ　＝　Ｂｆ
　　　　　　　Ｃｇ　＝　Ｃｆ
　　　　　　　Ｄｇ　＝　Ｄｈ
　　　辺々足して、
　　　　　　　（ Ａｅ ＋ Ｂｅ ）＋（ Ｃｇ ＋ Ｄｇ ） ＝ （ Ａｈ ＋ Ｂｆ ）＋（ Ｃｆ ＋ Ｄｈ ）
　　　よって、
　　　　　　　ＡＢ ＋ ＣＤ　＝　ＢＣ ＋ ＤＡ

　四角形が内接円を持つための必要十分条件は、
　　　　向かい合う辺の長さの合計が等しいことです。
　四角形の内心（ 内接円の中心 ）は、
　　　　各角の二等分線の交点です。

　四角形が外接円を持つための必要十分条件は、
　　　　向かい合う角の大きさの合計が等しいことです。
　四角形の外心（ 外接円の中心 ）は、
　　　　各辺の垂直二等分線の交点です。

円に内接する四角形の対角の和は 180 度 です。
　　　　
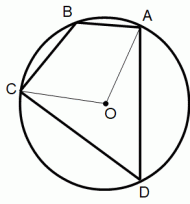
円周角の定理より、
　　　∠ＡＤＣ × ２　＝　∠ Ａ０Ｃ
　　　∠ＡＢＣ × ２　＝　∠ Ａ０Ｃ（ 外側 ）
辺々足して、
　　　（ ∠ＡＤＣ × ∠ＡＢＣ ）× ２　＝　360°
　　　よって、（ ∠ＡＤＣ × ∠ＡＢＣ ）× ２　＝　180°


では、 ここで問題です。 次の図において、 △ＡＢＣ と △ＡＥＤ が相似になっていることを示してください。

　　　　

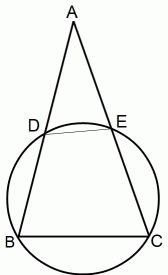
ヒントは、 ３つの角がすべて等しいことを示すことです。