病院のルームナンバーには、 4 と 9 の数字は用いられません。 では、 2000番目の病室のルームナンバーはいくらになるでしょうか?
1000毎に考えると、 400代 と 900代 は存在しないので 800 です。 100毎に考えると、 40代 と 90代 は存在しないので 80 です。 10毎に考えると、 4 と 9 は存在しないので 8 です。 したがって、 100毎に考えると、 80 −2×8 = 64 です。 1000毎に考えると、 64×8 = 512 です。 したがって、 2000番目の病室のルームナンバーは、 1024 になります。 ・ ・ ・ ・ ・ いいえ違います。 もし、 問題が「 ルームナンバーが 2000の病室は、 実際には何番目の部屋になりますか?」であればそれでいいのですが ・ ・ ・ ・ 。
いい考え方があります。 4 と 9 の数字がない代わりに、 8 と 9 の数字がなくても同じことであるというのが、 ヒントです。 そうですね、 8進法を使えばいいのです。 10進法を2進法に直すには、 どんどん2で割っていき、 その余りを逆さに並べるとよかったですね。 同様にして、 10進法の 2000 を8進法に変換します。
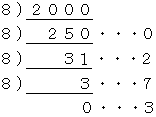
しかし、 答えは 3720 ではありません。 今は、 8 と 9 の数字がない場合で考えているのですが、 実際に考えなければならないのは 4 と 9 の数字がない場合です。 したがって、 答えは 3820 になります。
では、 ルームナンバーが 3820 の病室は何番目の部屋になっているでしょうか?
答えは次のようになります。
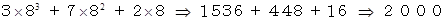
 数理論 へ戻る
数理論 へ戻る