（３） オームの法則の交流への拡張

　 次に、 オームの法則を交流回路に拡張すればどうなるであろうか？　答えは、「 電流や抵抗が、 複素数になる。」である。 虚数が意味するものは「 電流の位相の 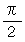のズレ 」である。 では、「 電流の位相のズレ 」とは何か考えてみよう。

交流は正弦波交流であり、 その電圧は次の式で表される。
　　　　
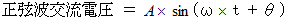
　 100 Ｖ の正弦波交流の場合、 電圧は 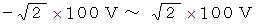の範囲で周期的に変動する。 は、 位相のズレ である。 位相がずれているために、 時刻 の瞬間の電圧が 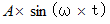とは異なっている。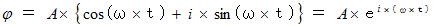
　　　　　
という波動関数があるとき、 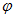を表す点は、 複素平面の原点を中心として、 半径 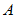の円の円周上を反時計回りに、 角速度 で等速円運動する。 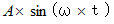は、 その点の運動の虚数軸への射影であり、 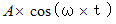は、 その点の運動の実数軸への射影である。 したがって、 が位相のズレであるといっても、 帯状のサインカーブにおける「 空間的なズレ 」ではなく、 ある位置における、「 時間的なズレ 」、 つまり、 シンクロナイズからの逸脱のことを言っているのだ。
　 電流が複素数になると言っても、 それは、 交流において常に変化している電流の周期運動の位相がズレルことを表しているのであって、 電流という物理量が本当に複素数になるわけではない。 物理学で登場する複素数は、 数学的手法上の便宜的な複素数なのである。 したがって、 抵抗が複素数になると言うのも、 同様に、 電流の位相をズレさせるような働きをするようになるということなのである。 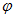からの位相のズレを表す は、 次の式を満たす である。
　

　 さあ、 以上の哲学的前提を確認した上で、 具体的な話に移ろう。
　 交流回路では、 次のような、 複素数の物理量たちが登場する。 これらは、 抵抗に相当するものであり、 単位は 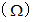である。

　　　インダクタ の 誘導リアクタンス ：　
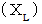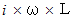
　　　キャパシタ の 容量リアクタンス ：　
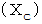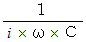
　　　インピーダンス ：　

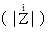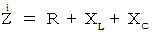
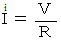が成り立つように、 　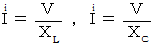が成り立つ。
頭に 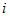を付けているのは、 複素数であるという意味である。

ではまず、「 抵抗とコイルとコンデンサを直列に繋いだ交流回路 」を考えよう。
　　　　
　　　　
　　　　
　　　　

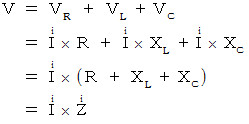
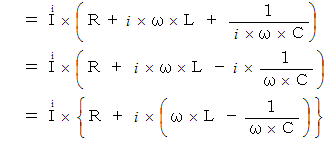
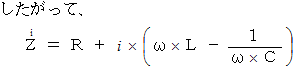
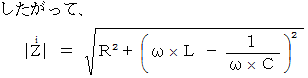
したがって、 電気回路全体の電流は次のように表される。
　　　　
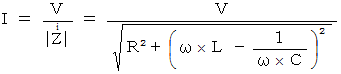
このとき、 電流の位相のズレは、 次の式を満たす で表される。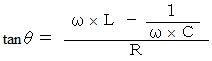
　　　　


次に、「 抵抗とコイルとコンデンサを並列に繋いだ交流回路 」を考えよう。
　　　　 　　　　
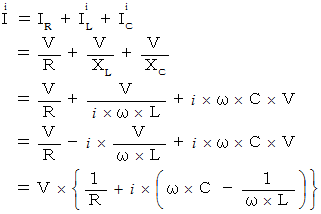
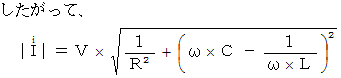
したがって、 電気回路のインピーダンス 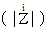は、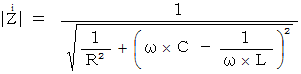
　　　　
このとき、 電流の位相のズレは、 次の式を満たす で表される。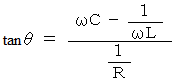
　　　　


　交流電圧の実効値 ：
　 交流電源が供給する平均電力と等しい量の電力を供給しつづける直流電源がある。 このとき、 この交流電源による電圧や電流の実効値は、 この直流電源による電圧や電流に等しい、 というのが実効値の定義である。 交流電圧の実効値は、 交流電圧の瞬時値の２乗の平均値の平方根であり、 最大交流電圧を 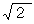で割った値である。 交流電流の実効値もこれと同様である。