ある数Ｐ について次の式が成り立ちます。 Ｐ はどんな数でしょうか？
　　　　　

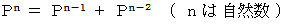
ｎ ＝ ２ のときを考えます。 すると次のようになります。
　　　　　
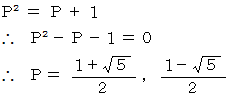
Ｐ の前者は 「 黄金比 」 と言われます。

　 本当に冒頭の式が成り立っているのかどうか、 十進BASIC のプログラムを作って確かめると、 そのとおりでした。

　　　　　
　　　　　
　　　　　


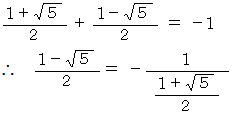
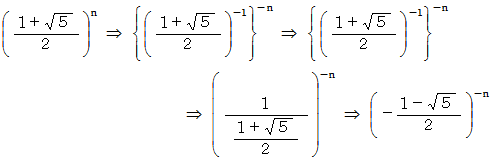
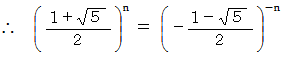
さて、 黄金比を 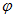として、 次のような数列を考えます。
　　　　　

この数列の漸化式は次のようになります。
　　　　　

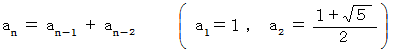
　 したがって、 この数列は、 准フィボナッチ数列であることがわかります。 そこで、 次のようなプログラムを作って実行すると、 具体的な数値として、 この順列を表すことができます。