(1) 波動方程式
 波動方程式( 帯状イメージバージョン)
波動方程式( 帯状イメージバージョン)サインカーブが右向きに等速移動しているイメージです。
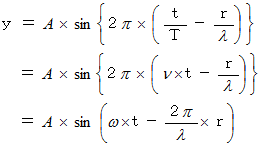
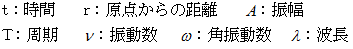
 波動方程式 ( 円盤イメージバージョン )
波動方程式 ( 円盤イメージバージョン )円周上を1点が反時計回りに等速円運動しているイメージです。 複素平面 を用いると、 波動方程式は次のようにも表現することができます。
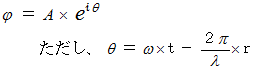
図−1
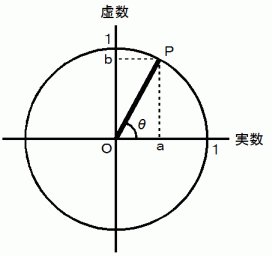
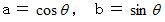
複素平面 では、 点
 の位置は次のように表されます。
の位置は次のように表されます。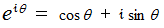
この式は、 オイラーの公式 と言われます。
円周上を点
 が反時計回りに等速円運動していると考えてください。 すると、 点
が反時計回りに等速円運動していると考えてください。 すると、 点  の等速円運動の実数軸への投影、 つまり、 点
の等速円運動の実数軸への投影、 つまり、 点  の運動は、 単振動です。
の運動は、 単振動です。 波動方程式( 双曲型偏微分方程式バージョン )
波動方程式( 双曲型偏微分方程式バージョン )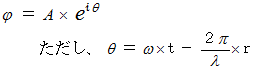
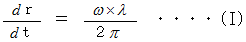
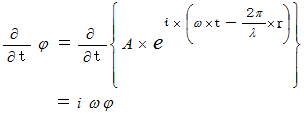
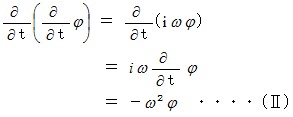
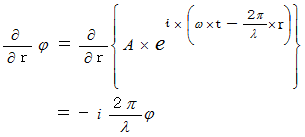
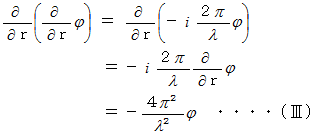
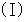 を
を 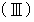 に代入すると、
に代入すると、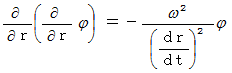
これに
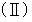 を代入すると、
を代入すると、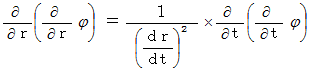
したがって、 次の式が成り立ちます。
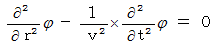
これが、 アカデミックな波動方程式です。
-
複素数
 , 自然対数の底
, 自然対数の底 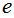 , 円周率
, 円周率  の定義は次のようになっています。
の定義は次のようになっています。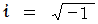
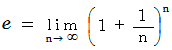
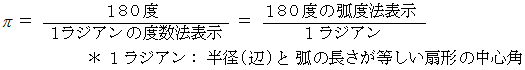
扇形の中心角は、 弧の長さの半径に対する比率で表されます
( 弧度法 )。
 は、 半円の弧の長さの半径に対する比率です。
は、 半円の弧の長さの半径に対する比率です。したがって、
 は 180度 の角度を表すものです。 また、 した
は 180度 の角度を表すものです。 また、 したがって、
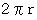 は円周の長さを表します。
は円周の長さを表します。オイラーの公式 :
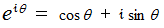 の
の  に
に  を代入すると、
を代入すると、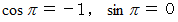 ですから、
ですから、 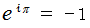 になります。
になります。これが、 数学で最も美しい式といわれる、 オイラーの等式です。 博士の愛した数式です。
オイラーの公式を導くには、 マクローリン展開を用います。
マクローリン展開 :
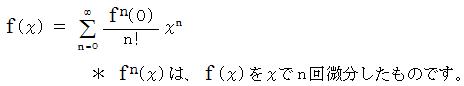
 より、
より、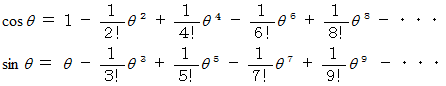
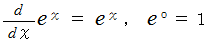 より、
より、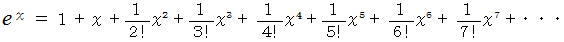
 に
に 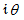 を代入して、
を代入して、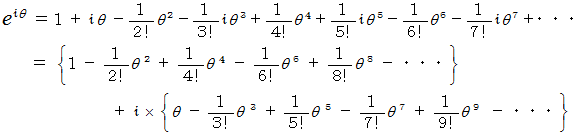
したがって、 次のオイラーの公式になります。
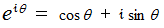
 三角関数 指数・対数関数 へ戻る
三角関数 指数・対数関数 へ戻る