 の逆関数を
の逆関数を 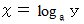 とする。
とする。
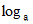 は、 常用対数 です。
は、 常用対数 です。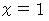 のとき、
のとき、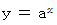 より、
より、 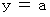
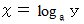 より、
より、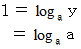
したがって、 一般的に、 次の式が成り立つ。
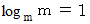
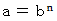 のとき、
のとき、
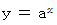 より、
より、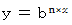

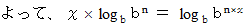 したがって、 一般的に、 次の式が成り立つ。
したがって、 一般的に、 次の式が成り立つ。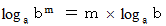
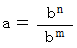 とする。
とする。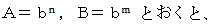
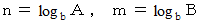


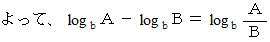
したがって、 一般的に、 次の式が成り立つ。
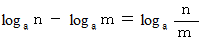
ここで、 常用対数関数 :
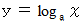 の微分を考える。
の微分を考える。
ここで、
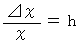 とおくと、
とおくと、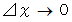 のとき、
のとき、 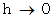 ,
, 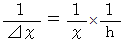 となる。
となる。したがって、

ここで、
 とおき、
とおき、 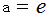 とすると、 次のようになる。
とすると、 次のようになる。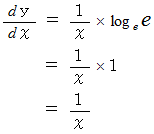
したがって、 一般的に、 次の式が成り立つ。
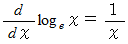
微分すると簡単な式で表される対数関数の底を求めて発見されたのが、 自然対数の底
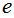 です。
です。 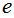 を発見したのも、 オイラー( 1707 〜 1783 ) なので、
を発見したのも、 オイラー( 1707 〜 1783 ) なので、 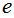 は、 オイラーの定数 とも言われています。
は、 オイラーの定数 とも言われています。 ) の起源
) の起源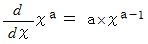 は正しいですが、
は正しいですが、 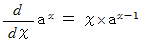 は間違いです。
は間違いです。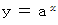 を微分してみましょう。
を微分してみましょう。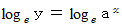
 で微分すると、
で微分すると、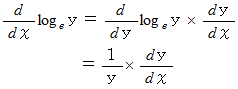
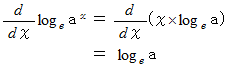
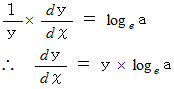
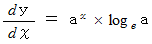
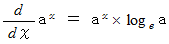
 に
に 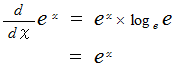
 この論文のトップへ戻る
この論文のトップへ戻る