「 素数
 と 正の整数
と 正の整数  がある。 それらの最大公約数が 1 であるならば、
がある。 それらの最大公約数が 1 であるならば、  は必ず
は必ず  で割り切れる。」 というのが、 フェルマーの小定理ですが、 オイラーは、 それを拡張することに成功しました。
で割り切れる。」 というのが、 フェルマーの小定理ですが、 オイラーは、 それを拡張することに成功しました。※ 参考: 数理論 > フェルマーの小定理
ある正の整数  よりも小さくて、 かつ、
よりも小さくて、 かつ、  との最大公約数が 1 である正の整数の数(かず)を
との最大公約数が 1 である正の整数の数(かず)を 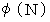 で表すとき、
で表すとき、 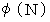 との最大公約数が 1 である任意の正の整数
との最大公約数が 1 である任意の正の整数  について、
について、 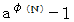 は必ず
は必ず  で割り切れる。
で割り切れる。
 よりも小さくて、 かつ、
よりも小さくて、 かつ、  との最大公約数が 1 である正の整数の数(かず)を
との最大公約数が 1 である正の整数の数(かず)を 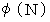 で表すとき、
で表すとき、 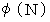 との最大公約数が 1 である任意の正の整数
との最大公約数が 1 である任意の正の整数  について、
について、 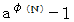 は必ず
は必ず  で割り切れる。
で割り切れる。これがオイラーの定理です。 なお、 この
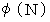 は、 オイラー関数と言われています。 彼は、
は、 オイラー関数と言われています。 彼は、  が素数のときは、 必ず
が素数のときは、 必ず  になることに注目したのです。 もし
になることに注目したのです。 もし  ならば、 7 よりも小さくて、 かつ、 7 との最大公約数が 1 である正の整数は、 1, 2, 3, 4, 5, 6 ですから、
ならば、 7 よりも小さくて、 かつ、 7 との最大公約数が 1 である正の整数は、 1, 2, 3, 4, 5, 6 ですから、  となりますものね。
となりますものね。オイラーの定理を確かめるために、 十進BASIC でプログラムを作ってみました。
ちなみに、 ある正の整数
 よりも小さくて、 かつ、
よりも小さくて、 かつ、  との最大公約数が 1 である正の整数を小さい順に表示するプログラムは、 次のようになります。
との最大公約数が 1 である正の整数を小さい順に表示するプログラムは、 次のようになります。オイラーの定理から、 さらに次の定理を導くことができます。
-
2つの異なる素数 p と q をかけた数 N がある。
N 未満の自然数 a がある。
a の ( p−1 )( q−1 ) + 1 乗 を N で割った余りは a である。
JavaScript のプログラムで確かめてみましょう。
プログラムの内容 :
【 問 題 1 】
-
2つの異なる素数 p と q がある。 N = pq である。
1 〜 N までの自然数で N と互いに素の自然数の数を求めよ。
-
1 〜 N までの自然数で 明らかに N と互いに素でないのは、 N の 1 個。
それ以外に N と互いに素でないのは、
p, 2p, 3p, ・ ・ ・ ・ , ( q − 1 )p の ( q − 1 ) 個 と、
q, 2q, 3q, ・ ・ ・ ・ , ( p − 1 )q の ( p − 1 ) 個 で、
その他には存在しない。
したがって、 答えは、
N − 1 − ( q − 1 ) − ( p − 1 )
=→ pq − p − q + 1
=→ ( p − 1 ) ( q − 1 )
-
n で割ると 1 余る自然数 m がある。 この数に n より小さな自然数 k をかけた数は n で割ると k 余ることを示せ。
-
m = an + 1 と置くと、 km = akn + k
k < n より、 km は n で割ると k 余ることが解る。
 数理論 へ戻る
数理論 へ戻る