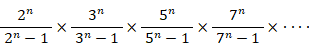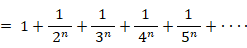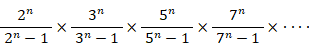
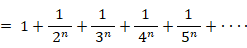
この式を証明しよう。
初項が 1 公比が r ( −1 < r < 1 ) の無限数列の和は、次のように収束する。

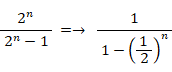 だから、
だから、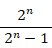 は、初項が 1 公比が
は、初項が 1 公比が  の無限数列の和である。よって、次の式が成り立つ。
の無限数列の和である。よって、次の式が成り立つ。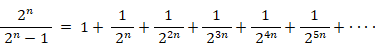
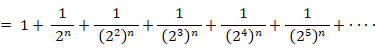
同様にして、次の式たちも成り立つ。
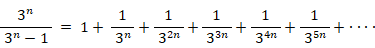
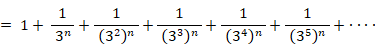
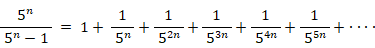
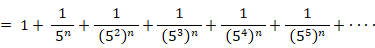
( あとは省略 )
オイラー積は次の式で表される。
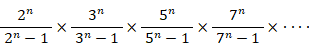
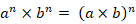 であり、2以上のすべての自然数は素数そのものか素数の積で表されるので、次の式が成り立つ。
であり、2以上のすべての自然数は素数そのものか素数の積で表されるので、次の式が成り立つ。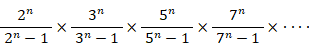
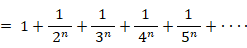
 数理論 へ戻る
数理論 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る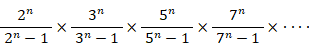
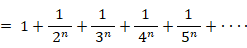

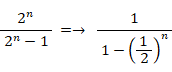 だから、
だから、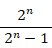 は、初項が 1 公比が
は、初項が 1 公比が  の無限数列の和である。よって、次の式が成り立つ。
の無限数列の和である。よって、次の式が成り立つ。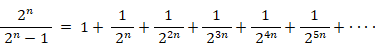
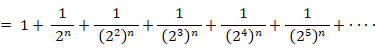
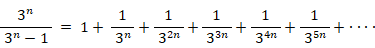
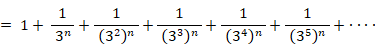
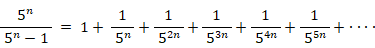
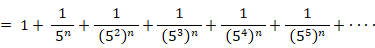
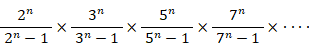
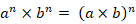 であり、2以上のすべての自然数は素数そのものか素数の積で表されるので、次の式が成り立つ。
であり、2以上のすべての自然数は素数そのものか素数の積で表されるので、次の式が成り立つ。