( 問 1 )
 を満たす
を満たす  の値をすべて求めなさい。
の値をすべて求めなさい。-
方程式は
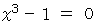 とも書けます。
とも書けます。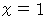 は明らかです。 したがって、
は明らかです。 したがって、 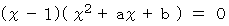 の形に持っていくことができ、 そうすれば他の解も求めることができます。
の形に持っていくことができ、 そうすれば他の解も求めることができます。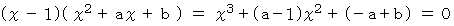
この式が
 についての恒等式になるためには、 次の条件を満たせばいいことになります。
についての恒等式になるためには、 次の条件を満たせばいいことになります。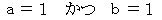
したがって、
 は次のように書くこともできます。
は次のように書くこともできます。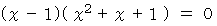
2次方程式の解の公式 :
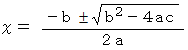 を使うと、 この式は次のようにも書くことができます。
を使うと、 この式は次のようにも書くことができます。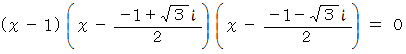
ただし、 この式の左辺は因数分解とはいいません。 この問題の答えは次のようになります。
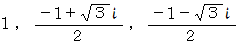
ここで、
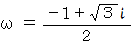 と置きます。 すると、
と置きます。 すると、 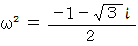 になります。
になります。また、
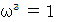 、
、 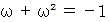 です。 したがって、 次の式が成り立ちます。
です。 したがって、 次の式が成り立ちます。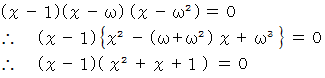
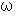 と
と 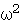 は
は 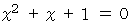 の解ですから、 次の式たちが成り立ちます。
の解ですから、 次の式たちが成り立ちます。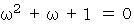
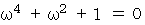
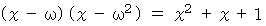
また、
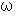 と
と 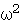 は
は  の解でもあるのですから、 次の式たちが成り立ちます。
の解でもあるのですから、 次の式たちが成り立ちます。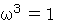
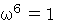
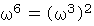 ですから、
ですから、 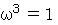 ならば必ず
ならば必ず 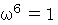 なので、
なので、 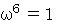 を省くことができます。
を省くことができます。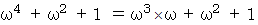 ですから、
ですから、 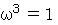 ならば必ず
ならば必ず なので、
なので、 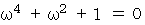 も省くことができます。
も省くことができます。この
 の3つの性質を利用すると、 高次式の因数分解式を発見することができることがあります。
の3つの性質を利用すると、 高次式の因数分解式を発見することができることがあります。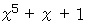 を因数分解しなさい。
を因数分解しなさい。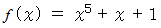 とおくと、
とおくと、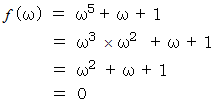
したがって、
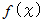 は次のように書くことができる。
は次のように書くことができる。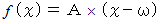
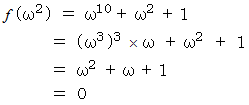
したがって、
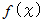 は次のように書くことができる。
は次のように書くことができる。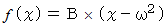
以上の2つより、
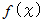 は次のように書くことができる。
は次のように書くことができる。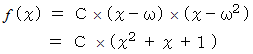
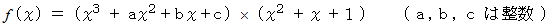 と置くと、
と置くと、 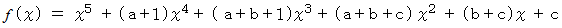
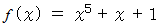 なので、 上の式が
なので、 上の式が  についての恒等式になるためには、 次の条件を満たせばいいことになる。
についての恒等式になるためには、 次の条件を満たせばいいことになる。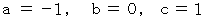
したがって、
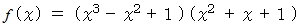
さらに
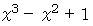 が因数分解できないかどうか検討する。
が因数分解できないかどうか検討する。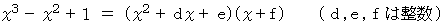 と仮定すると、
と仮定すると、
これが
 についての恒等式になるための条件は、 次のようになる。
についての恒等式になるための条件は、 次のようになる。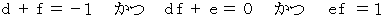
しかし、
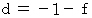 を
を  に代入すると、
に代入すると、 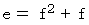 で、 これを
で、 これを 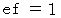 に代入すると、
に代入すると、 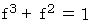 になって、 これを満たすような整数
になって、 これを満たすような整数 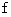 は存在しないことがわかる。 したがって、
は存在しないことがわかる。 したがって、 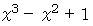 が因数分解できると仮定したことは間違いであった。
が因数分解できると仮定したことは間違いであった。とういうわけで、 結局、 この問題の答えは次のようになる。
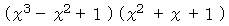
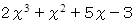 を因数分解しなさい。
を因数分解しなさい。-
χ = h( h は整数または簡単な分数 )のとき、 この式が 0 になるのなら、 この式は次のような形にすることができます。
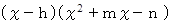
h の見つけ方ですが、 次の式を満たす数であることが必要条件になります。

したがって、 h の候補になる数は、 次の8つです。
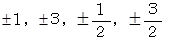
すると、
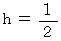 であることがわかります。
であることがわかります。そこで、 問題の式は次のように書くことができます。
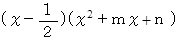
これは、 次のように書くこともできます。
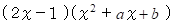
この式は、 次のように展開されます。
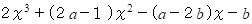
この式と問題の式の係数をそれぞれ比べると、
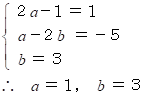
したがって、 答えは、
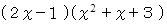
 その他の数学 へ戻る
その他の数学 へ戻る