 を満たす
を満たす  の値は、
の値は、  と
と  と
と 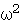 です。 ただし、
です。 ただし、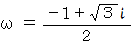 、
、 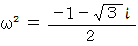 です。
です。 と
と 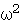 は、 それぞれ次のようにも表されます。
は、 それぞれ次のようにも表されます。
なぜなら、 次の式たちが成り立つからです。


 と
と  と
と 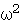 の複素平面上の位置は、 それぞれ図のようになります。
の複素平面上の位置は、 それぞれ図のようになります。
大きさが
 の複素数を掛けるという演算は、 複素平面では、 原点を中心とする半径
の複素数を掛けるという演算は、 複素平面では、 原点を中心とする半径  の円周上を、 実数軸の正の方向からの角度だけ反時計回りに回転させるということになりますので、 この図を見れば、
の円周上を、 実数軸の正の方向からの角度だけ反時計回りに回転させるということになりますので、 この図を見れば、  ,
,  ,
,  などは一目瞭然です。
などは一目瞭然です。複素数どうしを足すということは、 複素平面では、 実数軸と虚数軸との値を別々に加えることですから、 この図を見れば、 下の式が成り立っていることは一目瞭然です。
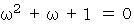
複素平面の原点から ω へ向かう複素ベクトルを
 で表し、原点から ω2 へ向かう複素ベクトルを
で表し、原点から ω2 へ向かう複素ベクトルを  で表すと、
で表すと、 +
+ は 原点から ( −1, 0 ) に向かう複素ベクトルになり、
は 原点から ( −1, 0 ) に向かう複素ベクトルになり、 ×
× は 原点から ( 1, 0 ) に向かう複素ベクトルになります。
は 原点から ( 1, 0 ) に向かう複素ベクトルになります。0 = x3−1 =→ ( x−1 )( x2+x+1 ) より、 x ≠ 1 のときは x2+x+1 = 0 、
その解が ω と ω2 だから、次の式が成り立ちます。
( x−ω )( x−ω2 ) = 0
この式を複素ベクトル的に表すと次のようになります。

よって、

この式を x2 + x + 1 = 0 と比較しても、
 +
+ = −1 かつ
= −1 かつ  ×
× = 1 になっていることがわかります。
= 1 になっていることがわかります。 +
+ = −1 より、
= −1 より、 や
や  の実数成分は 1/2 であることがわかり、
の実数成分は 1/2 であることがわかり、 や
や  の虚数成分は次の式から求めることができます。
の虚数成分は次の式から求めることができます。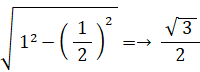
したがって、ω と ω2 はそれぞれ次のように表されます。
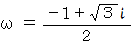
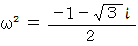
 数理論 へ戻る
数理論 へ戻る