※ 参照: 線形代数学 > 内積と外積
2次元平面では基底ベクトルどうしを掛けると別の基底ベクトルになります。ベクトルの掛け算の記号を & で表すと、具体的には次のようになります。 & は、外積でもない内積でもないベクトルの掛け算を表す演算子です。 & は、かけられるベクトルを、かけるベクトルの偏角ぶんだけ反時計回りに回転させて、かけるベクトルの大きさ倍にする演算子です。
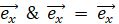
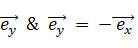
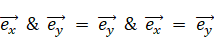
全体集合を大きさが 1 の平面ベクトルとします。すると、ベクトルは基底
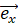 からの偏角 θ を用いて、一般に次のように表わされます。
からの偏角 θ を用いて、一般に次のように表わされます。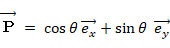
ガウス平面では、上式に相当するのが下式になります。
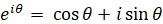
今、次の2つのベクトルがあります。
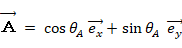
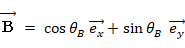
これらのベクトルのかけ算は次のようになります。
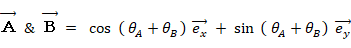
その理由を示します。
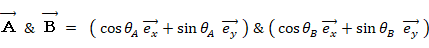
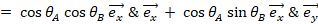
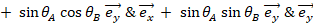
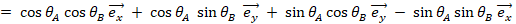
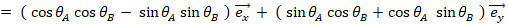
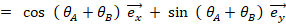
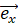 以外で2乗すると
以外で2乗すると 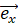 になるベクトル ( ガウス平面では −1に相当します。 ):
になるベクトル ( ガウス平面では −1に相当します。 ):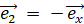
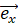 以外で3乗すると
以外で3乗すると 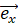 になるベクトル ( ガウス平面では ω に相当します。 ):
になるベクトル ( ガウス平面では ω に相当します。 ):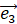
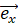 以外で4乗すると
以外で4乗すると 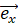 になるベクトル ( ガウス平面では i に相当します。 ):
になるベクトル ( ガウス平面では i に相当します。 ):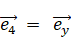
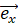 以外で n 乗すると
以外で n 乗すると 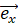 になるベクトル :
になるベクトル :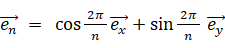
 数理論 へ戻る
数理論 へ戻る