（１） 正方形の折り紙を３等分する折り目を付ける方法

　 黄緑色をした一辺の長さが 1 cm の小さな正方形の折り紙 □ＡＢＣＤ を図のように折りました。

　　　　　　　
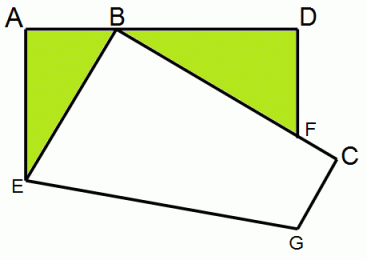
ＡＢの長さを x cm とすると、 ＤＦの長さはいくらになるでしょうか？

△ＡＥＢ と △ＤＢＦ は相似だから、
　　　　　

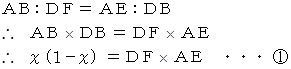
△ＡＥＢ におけるピタゴラスの定理より
　　　　　

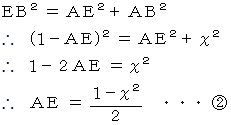
を に代入して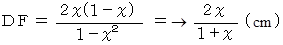
　　　　　

以上が答えです。


　
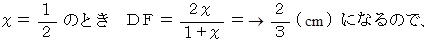
折り紙をちょうど ３分の １ に折り畳みたいときにこのことを利用するといいそうで、
これは 「 芳賀第１定理 」 と言われます。


では、 ついでにＧＣの長さも求めてみましょう。
△ＧＣＦ と △ＢＤＦ は相似だから、
　　　　　
　　　　　

（２） 正方形の折り紙の頂角を３等分する折り目を付ける方法

　 桃色をした一辺の長さが 30 cm の大きな正方形の折り紙 □ＡＢＣＤ を図のように折りました。
　　　　　　　　　　　　　　　　　（ ＧはＡＤの中点 )
　　　　　　　
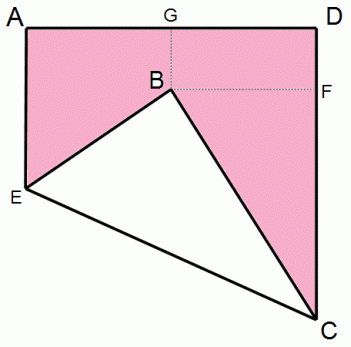
∠ＢＣＦの角度はいくらでしょうか？

∠ＢＣＦ ＝ θ 度 とすると、
　　　　　

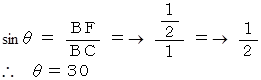
以上が答えです。

２ × ∠ＢＣＥ ＋ ∠ＢＣＦ　＝ 90度　より、　∠ＢＣＥ ＝ 30度 です。
このような方法で、 正方形の折り紙の頂角を３等分する折り目を簡単に付けることができます。