【 問 題 】

12×24 ｃｍ の長方形の紙を対角線で２つ折りにしたときに重なる部分の面積を求めよ。

【 解 答 】

　　　　　

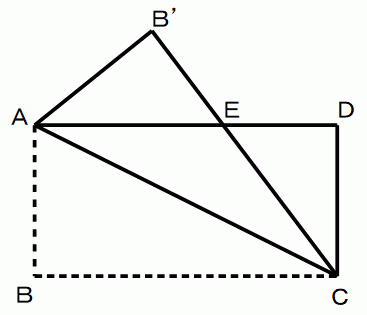
求めるのは、 △ＡＥＣの面積である。
△ＡＥＣの面積　＝　△ＡＤＣの面積 − △ＥＣＤの面積
△ＡＥＣ は二等辺三角形。　△ＡＢ'Ｅ と △ＣＤＥ は合同な直角三角形。
ＡＥ の長さを x ｃｍ とすると、
ＥＣ^２　＝　ＥＤ^２ ＋ ＣＤ^２　より、
x^２　＝　（ 24 − x ）^２ ＋ 12^２
よって、　x^２　＝　576 − 48x ＋ x^２ ＋ 144
よって、　x ＝ 15
したがって、
△ＥＣＤの面積　＝　｛ （ 24 − 15 ） × 12 ｝ ÷ ２　＝→　54
△ＡＥＣの面積　＝　△ＡＤＣの面積 − △ＥＣＤの面積
　　　　　　　　　　＝→　（ 24 × 12 ） ÷ ２　−　54　＝→　90（ ｃｍ^２ ）