【 問 題 】

縦の長さが a、横の長さが b の長方形の紙がある。

　　　

(1)　対角線で折った後に再び広げる。折ったときに重なっていた部分は菱形になっていることを示せ。

(2)　一対の対頂点が一致するように折った後に再び広げる。折ったときに重なっていた部分は菱形になっていることを示せ。

(3)　上記の２つの四角形は合同であるが、その面積を求めよ。

【 解 答 】

(1)




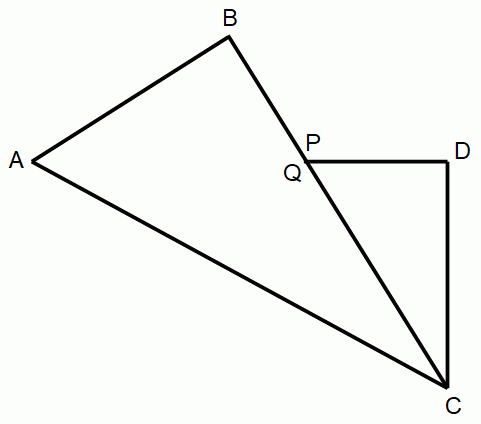
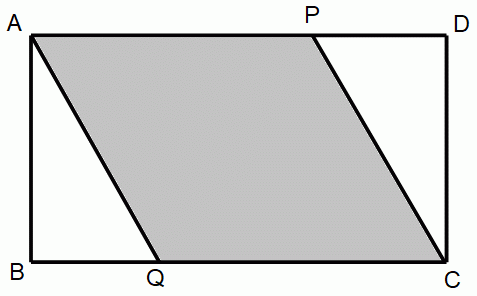
AC に対して対称だから、
　　∠APC = ∠AQC　　AP = AQ　　CP = CQ
∠CPD = AQB　　∠CDP = ∠ABQ　　CD = AB　より、
　　△CDP と △ABQ は合同である。
よって、
　　CP = AQ
よって、
　　AQ = QC = CP = PA
よって、
　　□AQCP は菱形である。



(2)




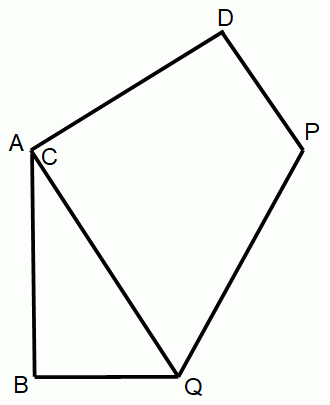
PQ に対して対称だから、
　　∠PAQ = ∠PCQ　　AP = CP　　AQ = CQ
∠QAB = ∠PCD　　∠ABQ = ∠CDP　　AB = CD　より、
　　△ABQ と △CDP は合同である。
よって、
　　AQ = CP
よって、
　　AQ = QC = CP = PA
よって、
　　□AQCP は菱形である。


(3)
　　AP = x　　PD = y　と置く
　　　　 x + y = b
　　　　 x² = a² + y²
　 　　　　= a² + ( b − x )²
　 　　　
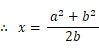
　　□AQCP = □ABCD − 2×△CDP
　　　　　　= a b − a y
　　　　　　= a ( b − y )
　　　　　　= a x
　　　　　　

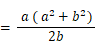
　　確かめ：
　　　　a = b のとき　□AQCP = a²