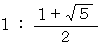
このことを証明しましょう。
1 辺の長さが 1 である正五角形ABCDEが円に内接しています。

円周角の定理より、 ∠AEB = ∠BEC = ∠CED です。
正五角形の頂角は 108 度です。 それは次の式から求めることができます。
( 180 度 × 3 )÷ 5 =→ 108 度
したがって、 ∠AEB = ∠BEC = ∠CED = 36 度 です。
対角線BE と 対角線AD の交点をFとします。
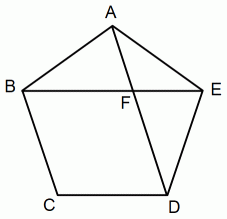
円周角の定理より、 ∠DAE = 36 度 です。
△FEAは二等辺三角形です。 FE = FA です。
∠AFE = 108 度 です。
∠BAF = ∠BFA = 72 度 です。
△BFAは二等辺三角形です。 BA = BF = 1 です。
△ABE と △FEA は相似です。
したがって、 AB : BE = FE : EA です。
FE = χ と置きます。
すると、 1 : 1+χ = χ : 1 になります。
よって、 χ2+χ = 1
よって、 χ2+χ−1 = 0
χ > 0 の範囲で上記の二次方程式を解の公式を用いて解くと、 次のようになります。
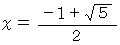
よって、
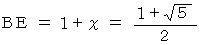
よって、
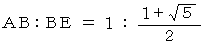
 幾何学 へ戻る
幾何学 へ戻る