モンテカルロ法を用いて円周率の近似値を求める方法は、 パソコンを用いずに実際の実験を行ってもよく、 そこのところが数学より物理学に近い所です。 しかし、 誤差が比較的大きく、 また実験に多大な時間がかかるのが欠点です。 そこで、 パソコンを利用して数学的な方法で誤差の小さい円周率の近似値を求めてみましょう。


（１） 平方数の逆数の和を用いる方法　（ ANSI/ISO/JIS 規格Ｃ言語 ）

　　　　

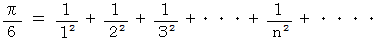
#include < stdio.h >
#include

main ( )
{
　　int i, n ;
　　double x, y ;
　　x = 0.0 ;
　　n = 1 ;
　　for ( i = 1 ; i <= 10000 ; i++ ) {
　　　　x += 1.0 / ( n * n ) ;
　　　　n++ ;
　　　　　　　　　　　　　　　　　　　　　}
　　y = sqrt ( 6.0 * x ) ;
　　printf ("円周率は %1.6f です。", y ) ;
　　return 0;
}

　　　　　表示される数は 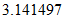であり、 けっこう誤差があります。
　　　　　

（２） マチンの公式を用いる方法　（ JIS Full Basic 言語 ）

　　　　

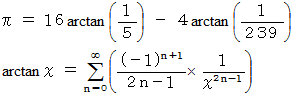
OPTION ARITHMETIC decimal_HIGH
LET X = 1 / 5
LET F = −X * X
LET T = X
LET S = 0
FOR J = 1 TO 1000
　　LET A = T / ( 2 * J − 1 )
　　LET S = S + A
　　LET T = F * T
NEXT J
LET Y = 1 / 239
LET B = −Y * Y
LET D = Y
LET E = 0
FOR K = 1 TO 1000
　　LET C = D / ( 2 * K − 1 )
　　LET E = E + C
　　LET D = B * D
NEXT K
PRINT "円周率は次のとおりです。"
PRINT 16 * S - 4 * E
END

　　　　　　表示される数は次のような小数点以下1007桁の数です。
　　　　　3.14159265358979323846264338327950288419716939937510
　　　　　5820974944592307816406286208998628034825342117067982
　　　　　1480865132823066470938446095505822317253594081284811
　　　　　1745028410270193852110555964462294895493038196442881
　　　　　0975665933446128475648233786783165271201909145648566
　　　　　9234603486104543266482133936072602491412737245870066
　　　　　0631558817488152092096282925409171536436789259036001
　　　　　1330530548820466521384146951941511609433057270365759
　　　　　5919530921861173819326117931051185480744623799627495
　　　　　6735188575272489122793818301194912983367336244065664
　　　　　3086021394946395224737190702179860943702770539217176
　　　　　2931767523846748184676694051320005681271452635608277
　　　　　8577134275778960917363717872146844090122495343014654
　　　　　9585371050792279689258923542019956112129021960864034
　　　　　4181598136297747713099605187072113499999983729780499
　　　　　5105973173281609631859502445945534690830264252230825
　　　　　3344685035261931188171010003137838752886587533208381
　　　　　4206171776691473035982534904287554687311595628638823
　　　　　5378759375195778185778053217122680661300192787661119
　　　　　590921642019893809511

　　　　　小数点以下1006桁目で初めて、 ２のところが １ となり、 誤差が出ます。



（３） プログラムの内容　（ Copy & Paste 用 ）

　※ 参照 ：
　　　　大学生のための数学 ＞ 解析学 ＞ 無限級数を利用して求める π の近似値
　　　　十進BASIC ＞ 十進BASIC＿算数 ＞ 円に内接する正多角形の面積から π の近似値を求める