【 問 題 】

大きな円の中に２つの図形がある。
大きな円の円周上に２点ＥとＦを取り、この２点を結ぶ線分ＥＦを描くとき、この線分は２つの図形の面積をそれぞれに２等分する。
そういった線分が必ず存在することを証明せよ。

　　

【 解 答 】

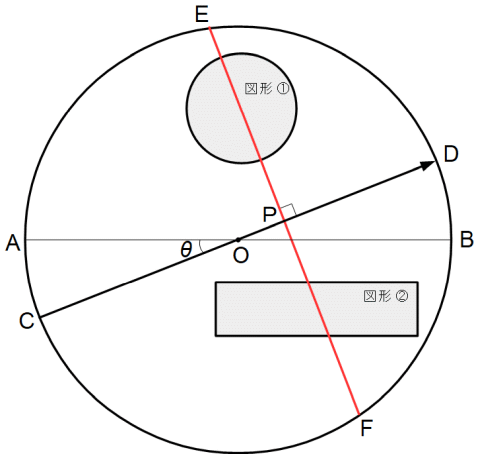
上図のように、
直径ＡＢ と 円の中心を通るベクトルＣＤ を描く。
線分ＥＦはベクトルＣＤに垂直であるとする。
ＣＤベクトルの直径ＡＢに対する偏角を θ ラジアン とする。
ＯＰの長さ（ 方向を持たせる ）を x とする。（ ＣＤベクトルの方向を正とする ）


　　

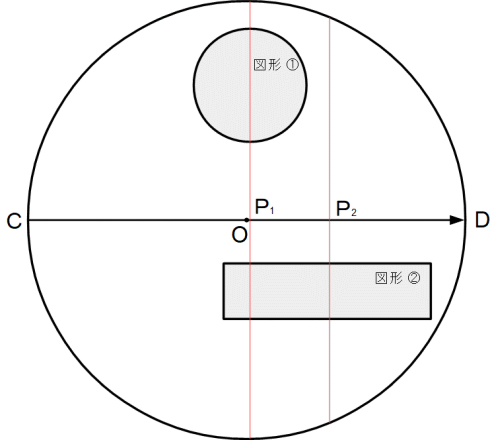
　０ ≦ θ ≦ π の範囲で θ を変化させたとき、（ 上図は θ ＝ 0 の場合 ） 図形 �@ を２等分するＣＤベクトルに垂直な線分の原点からの距離 P₁(θ) と 図形 �A を２等分するＣＤベクトルに垂直な線分の原点からの距離 P₂(θ) との関係について考える。
F(θ) ＝ P₁(θ) − P₂(θ)　という連続関数を考える。
F(0) ＝ P₁(0) − P₂(0)
F(π) ＝ P₁(π) − P₂(π)　＝→　−P₁(0) ＋ P₂(0)　＝→　−F(0)
F(π) ＝ 0 のとき、
　　P₁(0) ＝ P₂(0)　→　これは、直線ＡＢに垂直なある線分が２つの図形の面積をそれぞれに２等分することを意味している。
F(π) ≠ 0 のとき、
　　中間値の定理より、0 ＜ α ＜ π の範囲で、F(α) ＝ 0 を満たす α が存在する。
　　F(α) ＝ P₁(α) − P₂(α) ＝ 0
　　よって、 P₁(α) ＝ P₂(α)
　　これは、ＣＤベクトルの偏角が α ラジアン のときに ＣＤベクトルに垂直なある線分が２つの図形の面積をそれぞれに２等分すことを意味している。

　というわけで、「大きな円の円周上に２点ＥとＦを取り、この２点を結ぶ線分ＥＦを描くとき、この線分は２つの図形の面積をそれぞれに２等分する。そういった線分が必ず存在する。」ということが証明された。