問 題 :
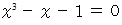 の3つの解を
の3つの解を 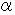 ,
, 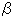 ,
, 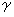 とするとき、
とするとき、(1)
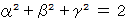 になることを示せ。
になることを示せ。(2)
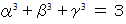 になることを示せ。
になることを示せ。(3)
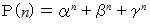 とすると、
とすると、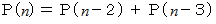
となることを示せ。
-
題意より、 恒等式 :
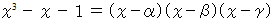 が成り立つ。
が成り立つ。この恒等式の右辺は、 次のようになる。
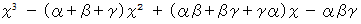
したがって、 次の3つの式が成り立つ。
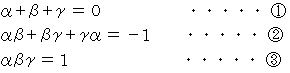

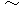
 より、
より、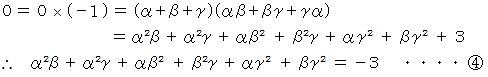
(1) の答え
 より、
より、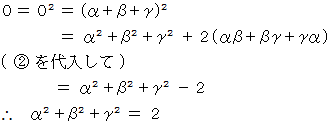
(2) の答え
 より、
より、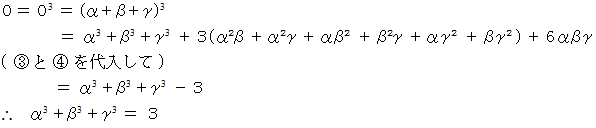
(3) の答え
 と (1) と (2) より、
と (1) と (2) より、 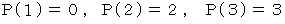
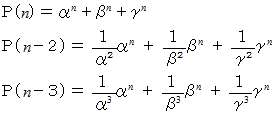
したがって、
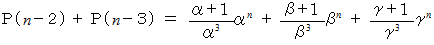
ここで、
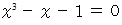 より、
より、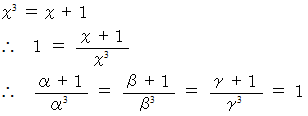
よって、
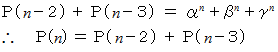
-
第
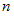 項の値
項の値 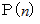 が
が 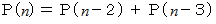 と表される数列は、 ペラン数列 と言われます。
と表される数列は、 ペラン数列 と言われます。 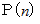 が
が 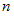 で割り切れるとき、
で割り切れるとき、 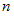 は素数だそうです。 これを確かめるため、 次のようなプログラムを Javascript で作ってみました。
は素数だそうです。 これを確かめるため、 次のようなプログラムを Javascript で作ってみました。< 上記のプログラムの実行結果 >
-
ペラン数列 : 0 2 3 2 5 5 7 10 12 17 22 29 39 51 68 90 119 158 209 277
第 n 項の数が n で割り切れるケース :
-
( 第 n 項, 第 n 項の数 ) =
( 2, 2 ) ( 3, 3 ) ( 5, 5 ) ( 7, 7 ) ( 11, 22 ) ( 13, 39 ) ( 17, 119 ) ( 19, 209 )
 数理論 へ戻る
数理論 へ戻る