自然対数の底である ネイピア数 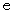は およそ の無理数である。 ネイピア数の定義は次の式である。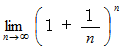
　　　　　
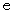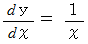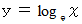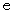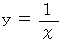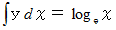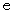　 ネイピア数 は、 で微分すると になる対数関数 の底 として定義されている。 つまり、 を で積分して得られる対数関数 の底 として定義されている。 （ 詳細は、 三角関数 指数・対数関数 ＞ おいらの愛した波動方程式 の（３）をご覧ください。）

ネイピア数 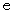は、 また、 次のようにも表される。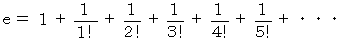
　　　　
その理由を考えてみよう。

マクローリン展開 ：
　　　　
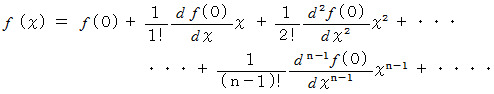
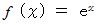のとき、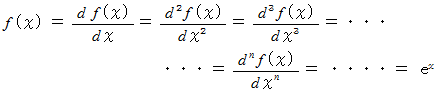
　　　　
　　　　

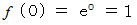
したがって、 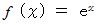のとき、 マクローリン展開は次のようになる。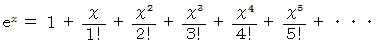
　　　　
この式に 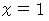を代入すると、 次のようになる。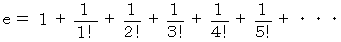
　　　　


次は、今とは違う導き方です。
ネイピア数 e は次のように定義されます。
　　
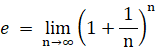
この式から次の式を導いてみましょう。
　　
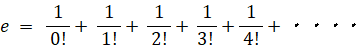
二項定理を用います。
　　
　　　　　　　　　　
　　　　
　　　　　　　　　　
　　　　
　　　　　　　　　　
　　　　
　　　　



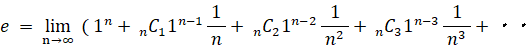
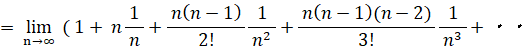
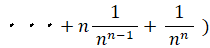
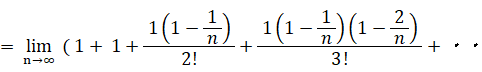
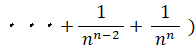
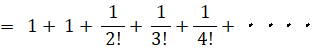
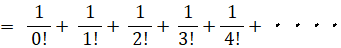
　複利で年利が１の預金とは、１年ごとに預金額が１年前の２倍になっていく預金のことです。１円からスタートすると、１年後に２円、２年後に４円、３年後に８円、・・・ と n 年後には ２ⁿ 円になります。
　一方、複利で 1/n 年利が 1/n の預金は、 1/n 年ごとに預金額が (1＋1/n) 倍になっていきます。例えば、n＝2 の時は、１年後の預金は (3/2)² ＝→ 2.25 円になり、n＝4 の時は、１年後の預金は (5/4)⁴ ≒→ 2.44 円 になります。ということは n を無限大にすると、１年後の預金額は無限大になるのではないでしょうか？ 考えてみましょう。１年後の預金額は次の式で与えられます。
　　　
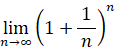
これはネイピア数です。ということは、n を無限大にしても１年後には預金額は 2.72 円にしかならないということです。