【 問 題 】

　　　

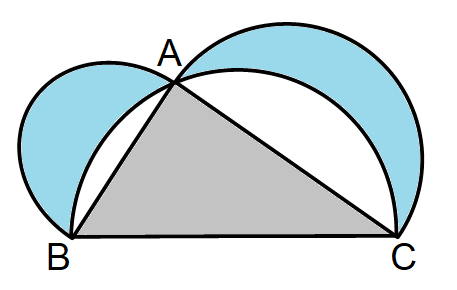
上図は３つの半円で作られた図に着色したものである。
水色の部分の面積 と 灰色の部分の面積 は等しいことを証明せよ。

【 解 答 】

　水色の部分の面積は、ＡＢを直径とする半円の面積 と ＡＣを直径とする半円の面積 と 三角形ＡＢＣの面積 とを加えたものから ＢＣを直径とする半円の面積 を引いたものに等しい。また、円周角の定理より、三角形ＡＢＣの頂角Ａは 90°である。
　したがって、辺ＡＢの長さを 2c 、辺ＢＣの長さを 2a 、辺ＡＣの長さを 2b とすると、水色の部分の面積は次のように表される。
　　　( π c² ＋ π b² ＋ 1/2 × 2b × 2c ) − π a²
　　　　　　　　　　　　　　＝→　π ( c² ＋ b² − a² ) ＋ 2bc
　　　　　　　　　　　　　　＝→　π { c² ＋ b² − ( c² ＋ b² ) } ＋ 2bc
　　　　　　　　　　　　　　＝→　2bc
直角三角形ＡＢＣの面積は 2bc である。
よって、水色の部分の面積 と 灰色の部分の面積 は等しい。