「 下図において、 答えも同時に記しているが、 頂点から各交点まで、 道を通って最短距離で進む方法は、 何通りあるか？ 」 いう問題があります。

　　　　　　　　

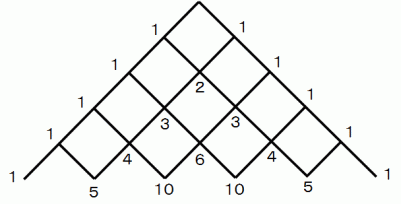
　３段目（ ３コマ進む ）までならすぐに解りますが、 ４段目（ ４コマ進む ）以上になると難しくなってきます。 そこで、 コツをお教えしましょう。 目的の交点まで進むには、 最後にその交点の 右斜上の交点から行く か 左斜上の交点から行く かのどちらかですので、 目的とする交点の右斜上の交点における最短距離で進む場合の数 と その交点の左斜上の交点における最短距離で進む場合の数 とを加えたものが、 求める答えになります。 頂点に を与えて、 以上の答えを、 ボウリングのピンの配置のように並べたものが「 パスカルの三角形 」です。

　発想の転換により、 違った方法で答えが求まります。 例えば、 ４段目の中央の交点の場合、 ４コマ進むのですが、 その１コマの進み方は、 右斜下に進む か 左斜下に進む かの２通りしかありません。 また、 目的の交点に到達するまでには、 右斜下に進むのが必ず２回になっています。 したがって、 ４コマのうち右斜下に進むのが 何コマ目 と 何コマ目 になるのか、 その組み合わせの数を求めればいいことが解ります。 したがって答えは次のようになります。
　　　


　さて、 二項定理は次のようなものです。
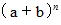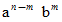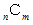　　　「 を展開したとき、 の係数は になる。」

例えば、 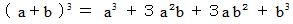　のとき、
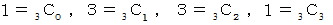　　　　です。

　「 パスカルの三角形 」がどうして二項定理を表しているのか、 上記の２通りの解答をみると、 その理由が解るような気がします。

　二項定理については、　十進BASIC＿算数 ＞ 二項係数 と パスカルの三角形　や　確率 と 統計学 ＞ 確率の二項分布 （ 独立試行の反復確率 ）　もご覧ください。