【 問 題 】

線分AB は円の直径である。円周上の点D から線分AB に垂線を下した。

　　　

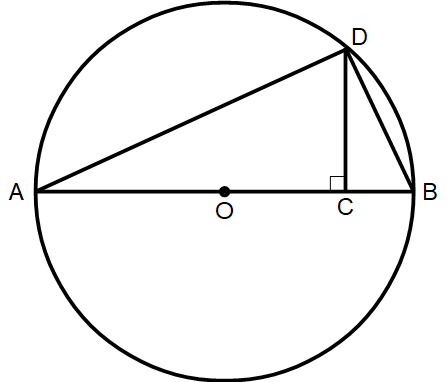
AC ＝ a　　BC ＝ b　　CD ＝ c　　とすると、 c² ＝ a×b　であることを証明せよ。

【 解 答 】

AD ＝ d　　BD ＝ e　　とすると、三平方の定理より、
　　　d² ＝ a² ＋ c²　　・・・ �@
　　　e² ＝ b² ＋ c²　　・・・ �A
　　　(a＋b)² ＝ d² ＋ e²　　・・・ �B

�Bより、 a² ＋ 2ab ＋ b² ＝ d² ＋ e²　　・・・ �C
�@と�Aを�Cに代入して、
　　　a² ＋ 2ab ＋ b² ＝ a² ＋ c² ＋ b² ＋ c²
　　　よって、
　　　　　　2ab ＝ 2c²
　　　よって、
　　　　　　c² ＝ a×b