ピタゴラスの定理
 幾何学 へ戻る
幾何学 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2025.04.05_____
三平方の定理の証明法を分類してみます。
【 1 】 タイルの敷き詰め法を用いる方法
(1) その他の数学 > 図は物語る
(2)
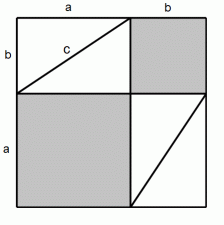
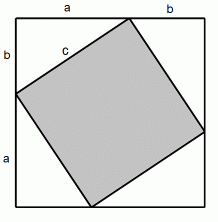
・ 両方の図を比べて、 a2 + b2 = c2
・ 右の図より、 c2 = (a+b)2−2ab
【 2 】 直角三角形を分割する方法
(1) ユークリッドによる証明法

AB = c BC = a CA = b CP = w
直角三角形ABC と 直角三角形PAC とは相似なので
b : w = a : b ⇒ b2 = aw ・ ・ ・ 
直角三角形PBA と 直角三角形PAC とは相似なので
c : ( a−w ) = a : c ⇒ c2 = a ( a−w ) ・ ・ ・ 

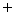
 より、 b2 + c2 = a2
より、 b2 + c2 = a2
(2) アインシュタインによる証明法

AB = c BC = a CA = b CP = w
直角三角形ABC と 直角三角形PAC と 直角三角形PBA は相似なので、
直角三角形PACの面積 = 直角三角形ABCの面積 × b2/a2
直角三角形PBAの面積 = 直角三角形ABCの面積 × c2/a2
直角三角形ABCの面積 = 直角三角形PACの面積 + 直角三角形PBAの面積 より、
1 = b2/a2 + c2/a2
よって、 b2 + c2 = a2
(3) 幾何学 > 三角形の内接円
(4) 無限等比級数の和の公式を利用する方法
直角三角形 AОB が直交座標系の上に置いてあります。点Aの位置する座標は( 0, a )で、点Bの位置する座標は( b, 0 )です。線分ABの長さを c とします。
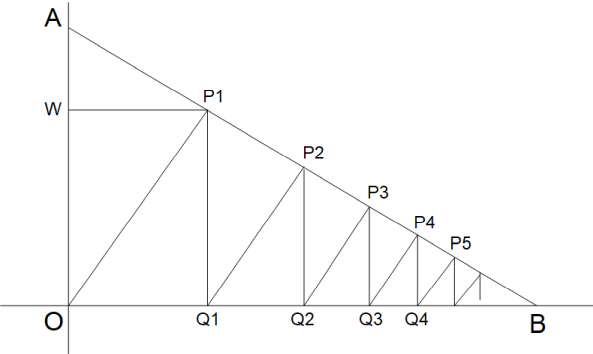
直角三角形 AОB と ОP1B とは相似です。
したがって、
AО : BA = ОP1 : BО
よって、 ОP1 = BО × AО ÷ BA =→ ab / c
また、 ОB:BA = P1B : BО
よって、 P1B = OB2 ÷ BA =→ b2 / c
直角三角形 AОB と AP1О は相似です。
直角三角形 AP1О と P1WО は相似です。
よって、 直角三角形 AОB と P1WО は相似です。
したがって、 AО : BA = P1W : ОP1
よって、 P1W = ОP1 × AО ÷ BA =→ ОP1 × ( a / c )
直角三角形 P1WО と ОQ1P1 は合同です。
したがって、 ОQ1 = P1W =→ ОP1 × ( a / c ) =→ b × ( a / c )2
直角三角形 AОB と P1Q1B は相似です。その相似比は c : b2 / c です。
直角三角形 P1ОQ1 と P2Q1Q2 とは相似です。その相似比は c : b2 / c です。
したがって、 ОQ1 : Q1Q2 = 1 : b2 / c2
よって、 Q1Q2 = ОQ1 × b2 / c2 =→ b × ( a / c )2 × ( b / c )2
同様に考えると、 Qn-1Qn : QnQn+1 = 1 : b2 / c2 ですので、
QnQn+1 = Qn-1Qn × ( b / c )2
したがって、次の等式が成り立ちます。
b = ОQ1 + Q1Q2 + Q2Q3 + ・・・・
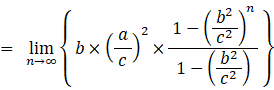 ※ 等比数列の和の公式
※ 等比数列の和の公式



したがって、 c2 − b2 = a2
よって、 a2 + b2 = c2
【 3 】 解析学的方法
ピタゴラスの定理の証明については、 次のホームページをお勧めします。
http://shochandas.xsrv.jp/index.htm
私的数学塾 > 私の備忘録 > 幾何学分野 > ピタゴラスの定理とその証明


 幾何学 へ戻る
幾何学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る





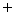
 より、 b2 + c2 = a2
より、 b2 + c2 = a2

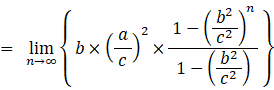 ※ 等比数列の和の公式
※ 等比数列の和の公式

