直線群が与えられたときに、 その全ての直線とどこかで接するような曲線のことを「 直線群の包絡線 」と言います。 したがって、 ある曲線のすべての接線となる直線群があるとき、 そのすべての直線に接するその曲線は、 その直線群の包絡線になります。

　 包絡線の方程式が 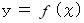で与えられているとき、 接線の方程式は任意（ 範囲がある場合もある ）の実数 ｔ を用いて次のように表されます。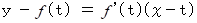
　　　　　
たとえば、 y ＝ x^２　という放物線の接線群は次のように表されます。
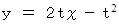　　　　　　（ ｔ は任意の実数 ）

　 直線群が任意（ 範囲がある場合もある ）の実数 ｔ を用いて表されているとき、 x を固定すると、 ｔ を変化させても y は変化しなので、 次の式が成り立ちます。
　　　　　
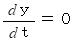
　 直線群 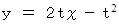：　　（ ｔ は任意の実数 ）　の包絡線を求めてみましょう。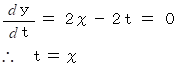
　　　　　
　　したがって、
　　　　　

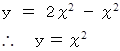
　 別の直線群 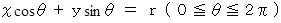：　　の包絡線を求めてみましょう。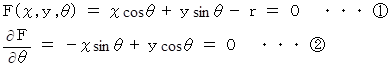
　　　　　
　　　　　
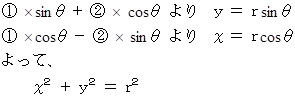
　　　　　これは、 半径 の円です。