( 問 題 1 )
-
いくつかの連続な自然数の和が1000であるとき、 この連続な自然数を求めよ。
( 山形大 1989年 入試問題 )
-
次のような十進BASICプログラムを作って解くと、 答えは 28 〜 52, 55 〜 70, 198 〜 202 の3つあることが解ります。
FOR i = 1 TO 9998
FOR j = i + 1 TO 1000
IF j^2 + j − i^2 + i = 2000 THEN
PRINT i ; " 〜 " ; j
END IF
NEXT j
NEXT i
END
このプログラムの根拠は次のようになっています。 答えを
 〜
〜  とします。
とします。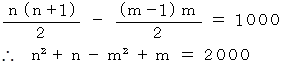
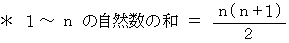
しかし、 試験ではこの解答は通用しません。 そこで次の問題2の解法をお勧めします。
-
2012 を 連続する自然数の和で表せ
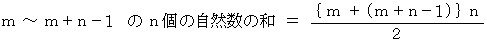
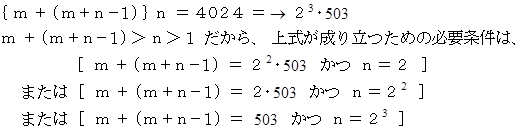
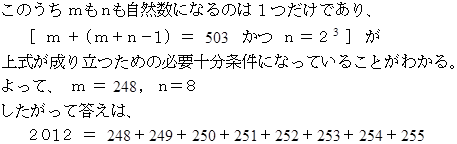
 数理論 へ戻る
数理論 へ戻る