（１）　連分数を利用したプログラム

　 無理数 の近似値を求める十進BASICのプログラムは、 次のように簡単なものです。

　　　10　LET N = 1
　　　20　LET M = 2
　　　30　FOR I = 1 TO 250
　　　40　 LET L = N
　　　50　 LET N = M
　　　60　 LET M = 2*M + L
　　　70　NEXT I
　　　90　PRINT USING "#.############": 1 + N/M ;
　　　100 END


このプログラムは、 次の連分数 を少数表示に変換しているのです。
　　　　

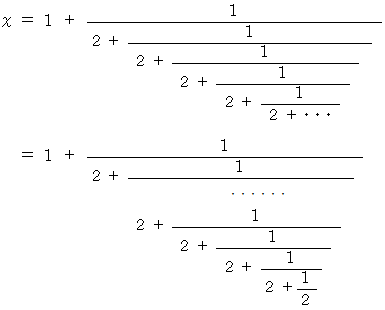
この連分数が であることの証明は、 次のようなものです。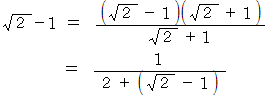

　　　　
　　　　したがって、
　　　　　　　　　　　　
　　　　　　　　　　　　
　　　　　　　　　　　　
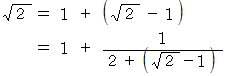
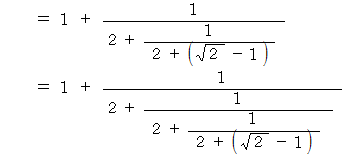
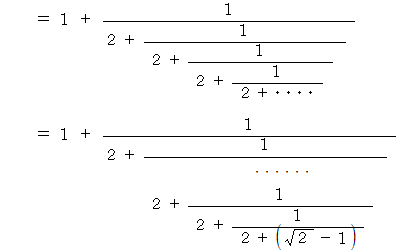
　 上の連分数の一番最後の 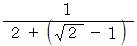の影響は小さいのでそれを とみなします。 すると、 この式は上記の を表す式と同じになります。

連分数 の一番最後から２番目の分数の分母を通分すると、 次のようになります。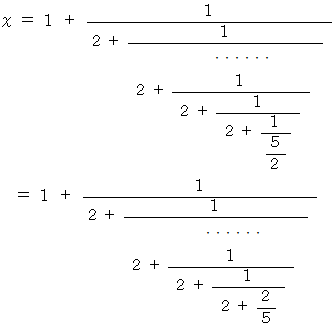
　　　　
　 この連分数の一番最後の分数 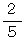をピックアップしたら、 さらにこの連分数の一番最後から２番目の分数の分母を通分して、 次のようにします。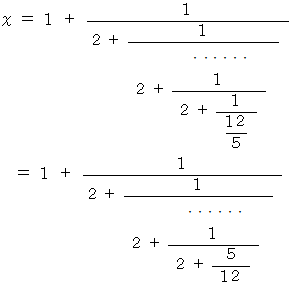
　　　　
　 この連分数の一番最後の分数 をピックアップしたら、 さらにこの連分数の一番最後から２番目の分数の分母を通分し ・ ・ ・ ・ 、 と同様なことを繰り返します。 そして、 ピックアップした連分数の一番最後の分数を並べて数列を作ると、 次のようになります。
　　　　　　

　 この数列の数の分母と分子には規則性があり、 前項の数の分母と分子を見れば次項の数の分母と分子が解るようになっています。 これが、 このプログラムの骨子です。