【 問 題 】
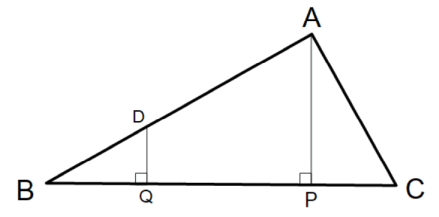
三角形ABCは直角三角形です。頂点Aから辺BCに垂線を下ろしその交点をPとします。
辺BC上に CP = BQ となるような点Qを取ります。
点Qを通り辺BCに垂直な直線が辺ABと交わる点をDとします。
CP = 1 BP = a とします。
APの長さとDQの長さを求めてください。
-
△ABC と △PBA と △PAC と △QBD とは相似になります。
△PBA と △PAC とが相似より、 PB:AP = PA:CP だから、
PA2 = PB × CP よって、 AP2 = a したがって、
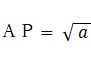
△PBA と △QBD とが相似より、 PB:AP = QB:DQ だから、
PB × DQ = AP × QB よって、
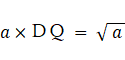
よって、
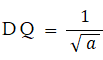
 幾何学 へ戻る
幾何学 へ戻る