（１） ローレンツ変換

　 ローレンツ変換は、 直交座標系 から 斜交座標系 への 位置ベクトルの座標変換です。 一般に、 直交座標系のベクトル空間から斜交座標系のべクトル空間へのベクトルの座標変換は、 座標変換テンソル 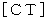を用いて次のような線形変換で表されます。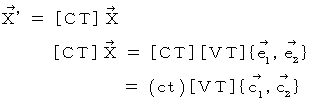
　　　　
　 基底変換テンソル 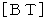の表現行列の逆行列は、 座標変換テンソル 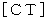の表現行列です。 したがって、 上式で表される座標変換の変換後のベクトル空間をイメージするには、 座標変換テンソル 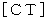の表現行列の逆行列を求めて、 それを基底変換テンソル 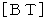の表現行列と見て、 斜交座標系の基底の要素となっているベクトルたちをイメージすればいいのです。 では、 次のような「 ベクトルの座標変換 」を例にとって、 変換後のベクトル空間をイメージしてみましょう。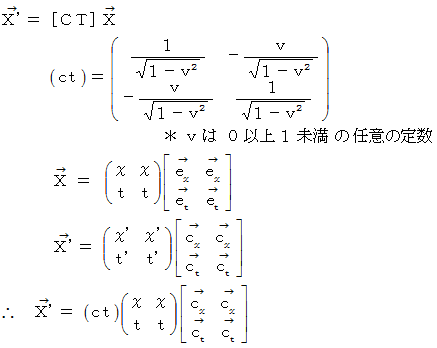
　　　　

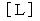　 この式のテンソルは、 ローレンツ変換テンソルです。（ 光の速さを とする単位系を用いています。 ）これを と表すことにします。 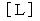は 座標変換テンソル 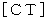です。 そして、 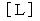の表現行列の逆行列は次のように表されます。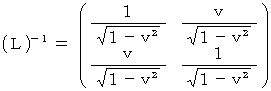
　　　　
　 このローレンツ変換における基底変換テンソル 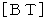の表現行列は 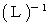ですので、 ローレンツ変換は次の基底の要素たちによって構成される斜交ベクトル空間への座標変換であることがわかります。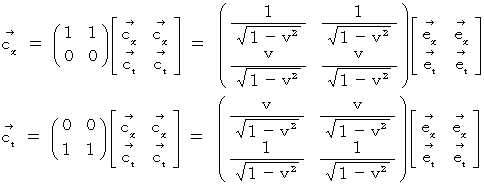
　　　　
　 したがって、 ローレンツ変換は、 直交時空間の空間軸と時間軸を近づけるように対称的に回転させた斜交時空間に変換するもので、 標準基底の要素たちを 倍の大きさに変化させます。 座標変換とは、 同一ベクトルの「 元の座標系の基底を用いた表現 」から「 変換後の座標系の基底を用いた表現 」への変換のことです。 したがって、 ローレンツ変換とは何か？ を、 次のように説明することができます。

　　　　

そこで、 相対性理論は、 次のように言います。
　「 空間軸と時間軸からなる時空平面をイメージしてください。 光の速さを とする単位系を用います。 また、 座標変換後の斜交時空間は元の直交時空間に対して速さ で移動しているものとします。 座標変換前の直交時空間と座標変換後の斜交時空間を重ねてください。 そして任意の時空点を１つ取り、 原点からその時空点に矢印を描いてください。 それがその時空点の位置ベクトルです。 この同一の位置ベクトルを、 静止している空間（ 直交時空間 ）の表示から、 移動している空間（ 斜交時空間 ）の表示へと、 書き換えを行うのが、 ローレンツ変換です。 たとえば、 時刻が で空刻が の時空点の位置ベクトルであれば、 次のように書き換えられます。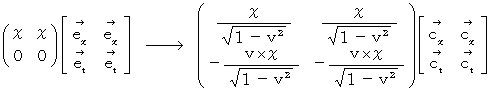
　　　　
　 上式の空間軸に注目してください。 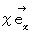　が　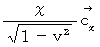 に変換されています。 これは成分どうしの比較で言えば、 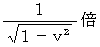になっています。 そうです、 ローレンツ変換（ ローレンツ変換は『 静止している空間の中で移動している空間 』を『 移動している空間の中で静止している空間 』へと変換させる道具です。）により、 観察の対象になっている空間は 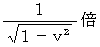に伸展するのです。
　 ところで、 元の直交時空間において、「 原点 」と「 空刻が の時空点 」で時刻 に同時に一瞬閃光が放たれたとしましょう。 この出来事が発生した時所を斜交時空間での表示にしますと、 １つの閃光は原点で時刻 に放たれますが、 もう１つの閃光が放たれる時刻は ではありません。 これは『 同時刻性の相対性 』と言われます。
　 さて、 同一の位置ベクトルは、 ２つの座標系で共通する『 発生した出来事 』を意味すると考えてください。『 移動している物質がその時その所に存在する。』というのも出来事の１つです。 ローレンツ変換テンソル 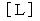は、『 出来事が発生する時空間位置 』を直交時空間表示から斜交時空間表示へと変換させるものです。 したがって、 ローレンツ変換という座標変換は、 普遍的な出来事が発生した時刻や場所が『 静止している空間 』と『 移動している空間 』でどのように観察され記載され、 それがどのように異なるのかを求める道具なのです。」


　 ローレンツ変換は、 次のような、 直交時空間から斜交時空間へのベクトルの座標変換です。
　　　　
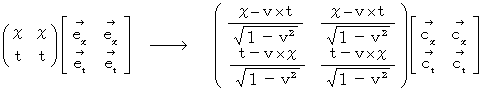
しかし、「 ローレンツ変換テンソル 」は、 次のような、 直交時空間のサイズを変化させる写像を担う「 演算テンソル 」であると、 しばしば誤解されます。
　　　　
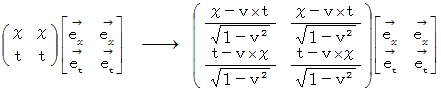
さらには、 ローレンツ変換は、 ベクトルの変換であることすら忘れられてしまって、 次のように、 単なる時空点の写像であるかのような誤使用をされることもあります。
　　　　
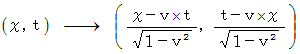
私などは、「 慣性系相対性理論の手引き 」という本の中で、 しばしばこの間違いをしています。

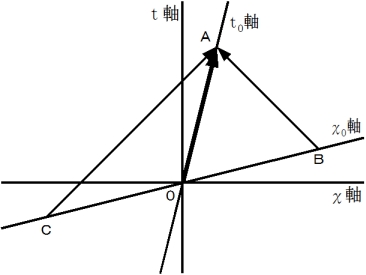
　図-４
　　　

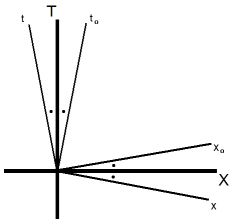
　 図-４ で言うと、 ローレンツ変換 と 逆ローレンツ変換 は次のような座標変換です。
　　　　ローレンツ変換　 ：　直交座標ＸＹ系　　　　斜交座標χ_０ｔ_０系
　　　　逆ローレンツ変換 ：　斜交座標χ_０ｔ_０系　　　直交座標ＸＹ系

　 これらの座標変換とは何か？ 哲学的に考えてみましょう。
　 １次元空間を思い浮かべてください。 物質Ａ と 物質Ｂ が相対的等速直線運動をしています。 Ａ君は物質Ａと並走しており、 Ｂさんは物質Ｂと並走しています。 また、 Ｃ君は彼らと別の速さで相対的等速直線運動をしています。 物質Ａ と 物質Ｂ は同時に時空原点を通過した後、 移動しているものとします。 この時、 ローレンツ変換 と 逆ローレンツ変換 は次のような内容になります。

　＜ ローレンツ変換 ＞
　　　　「 Ａ君による、 物質Ｂの時空間位置についての、 当事者的な主観的観察 」
　　　　「 Ａ君による、 物質Ｂの出来事についての、 第３者的な主観的観察 」
　　　　　　　　　　　　　　　　　　　　
　　　　「 Ａ君による、 Ｂさんの物質Ｂの時空間位置についての当事者的な主観的観察について
　　　　　の、 当事者的な客観的観察 」
　　　　「 Ａ君による、 物質Ｂの出来事についての、 当事者的な客観的観察 」

　　　　 直交座標ＸＹ系における物質Ｂの位置する時空間座標を次のように置くと、
　　　　　　　　　
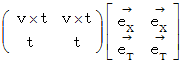
　 　　　斜交座標χ_０ｔ_０系における物質Ｂの位置する時空間座標は次のようになります。
　　　　　　　　　

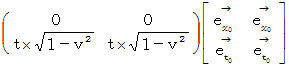
　　　　（ ローレンツ変換 の例 ）
　　　　　　「 Ａ君による、 物質Ｂの出来事についての、 第３者的な主観的観察（ 直交座標系 ）
　 　　　　　の内容 ：
　 　　　　　　物質Ｂが物質Ａを追い越した瞬間から今までの３０秒間で、 物質Ｂの温度が １０℃
　 　　　　　上昇した。」
　　　　　　　　　　　　　　　　　　　　　　
　　　　　　「 Ａ君による、 物質Ｂの出来事についての、 当事者的な客観的観察（ 斜交座標系 ）
　 　　　　　の内容 ：
　 　　　　　　物質Ｂが物質Ａを追い越した瞬間から今までの２０秒間で、 物質Ｂの温度が １０℃
　 　　　　　上昇した。」

　　　　　　＊ コメント：
　　　　　　　　　当事者的な観察 ：　観察の対象になる物質は静止している。
　　　　　　　　　第３者的な観察　：　観察の対象になる物質は移動している。
　　　　　　　　　主観的観察　： 　観察者に対して静止している物差しや時計を用いての観察。
　　　　　　　　　客観的観察　： 　観察者が見る、 観察の対象になる物質が携帯している物差
　 　　　　　　　　　　　　　　　　　しや時計を用いての観察。
　　　　　　　　　「 第３者的な主観的観察 」は、 ニュートン力学的な観察であり、
　　　　　　　　光速不変の原理に背きます。

　＜ 逆ローレンツ変換 ＞
　　　　「 Ａ君による、 Ｂさんの物質Ｂの時空間位置についての当事者的な主観的観察について
　　　　　の、 当事者的な客観的観察 」
　　　　「 Ａ君による、 物質Ｂの出来事についての、 当事者的な客観的観察 」
　　　　　　　　　　　　　　　　　　　　
　　　　「 Ａ君による、 物質Ｂの時空位置についての、 当事者的な主観的観察 」
　　　　「 Ａ君による、 物質Ｂの出来事についての、 第３者的な主観的観察 」

　　　　（ 逆ローレンツ変換 の例 ）
　　　　　　「 プラットホームにいる人による、 通過中の列車の中央にあるターゲットについての、
　 　　　　　当事者的な客観的観察（ 斜交座標系 ）の内容 ：
　 　　　　　　列車の前と後から同時に放たれた光が、 そのターゲットに同時に当たる。」
　　　　　　　　　　　　　　　　　　　　　　
　　　　　　「 プラットホームにいる人による、 通過中の列車の中央にあるターゲットについての、
　 　　　　　第３者的な主観的観察（ 直交座標系 ）の内容 ：
　 　　　　　　列車の前と後から異なる時刻に放たれた光が、 そのターゲットに同時に当たる。」


　　　　　

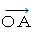　　　　　　　　　　 ：　ターゲットの、 プラットホームの人とすれ違ってから閃光が届くまで
　　　　　　　　　　　　　　　の、 軌跡
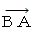　　　　　　　　　　 ：　列車の前から放たれた閃光の、 放たれてからターゲットに届くまで
　　　　　　　　　　　　　　　の、 軌跡
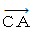　　　　　　　　　　 ：　列車の後から放たれた閃光の、 放たれてからターゲットに届くまで
　　　　　　　　　　　　　　　の、 軌跡


　 　　　　　　　　点 ， 点 ， 点 は、 座標変換にて、 その位置を変えません、 不動です。
　 　　　　　　　　斜交座標系では、 点 と 点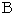 は同時刻ですが、 直交座標系では、 点 と
　　　　　　　　点 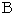は同時刻ではありません。
　 　　　　　　　　この図は、 プラットホームにいる人による、 ターゲットについての、 ニュー
　　　　　　　　トン力学的観察（ 直交座標系 ）と 相対論的観察（ 斜交座標系 ）の比較
　　　　　　　　を示すものであって、 プラットホームにいる人の座標系 と 列車の中にいる
　　　　　　　　人の座標系 の比較を示すものではありません。 この図は、 逆ローレンツ変
　　　　　　　　換 または ローレンツ変換 を表しています。