(2) 複素数ローレンツ座標変換
-
光の速さを
 とする単位系では、 ローレンツ変換は次のように表されます。
とする単位系では、 ローレンツ変換は次のように表されます。
ここで、 時間を虚数時間とします。 すると上式は次のように表されます。 座標変換テンソルの表現行列の中の虚数の成分の正負の符号に注意してください。
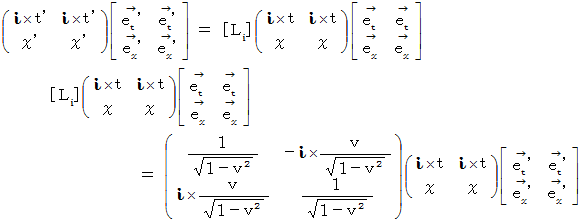
私は、 これを「 複素数ローレンツ座標変換式 」と言っています。
これから、 複素数ローレンツ座標変換が登場する過程を紹介します。
まず、「 複素数電磁場テンソル (
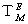 )」は次のようなものです。
)」は次のようなものです。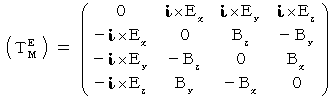
* ここでは、 本来の電場を光の速さで割ったものを、「 実質電場 」として
用いています。 光の速さを
 とする単位系では、 本来の電場が「 実質
とする単位系では、 本来の電場が「 実質電場 」を表します。
実質電場
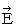 は、 電束密度
は、 電束密度 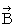 ( 私は、 これを「 実質磁場 」と言って
( 私は、 これを「 実質磁場 」と言っています。) と共に電磁場テンソルを構成します。
次に、 静止系の座標系 ( 第1観察者の座標系 ) の、 それに対してX軸方向に速さ
 で移動している運動系 ( 第0観察者の座標系 ) への「 複素数ローレンツ座標変換テンソル
で移動している運動系 ( 第0観察者の座標系 ) への「 複素数ローレンツ座標変換テンソル 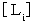 」の表現行列は、 次のように表されます。 ただし、 光の速さを
」の表現行列は、 次のように表されます。 ただし、 光の速さを  とする単位系を用いています。
とする単位系を用いています。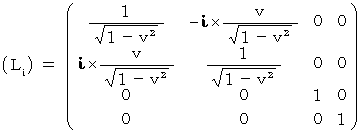
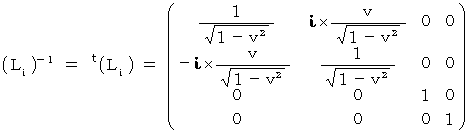
*
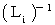 は
は 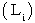 の 逆行列 です。
の 逆行列 です。 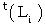 は
は 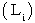 の 転置行列 です。
の 転置行列 です。第1観察者の時空点は、「 複素数ローレンツ座標変換テンソル
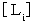 」により、 次のように第0観察者の時空点に変換されます。
」により、 次のように第0観察者の時空点に変換されます。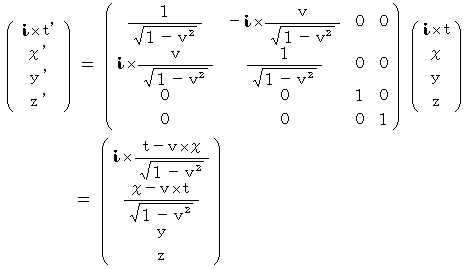
第1観察者の
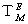 は、「 複素数ローレンツ座標変換テンソル
は、「 複素数ローレンツ座標変換テンソル 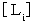 」により、 次のように第0観察者の
」により、 次のように第0観察者の 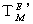 に変換されます。
に変換されます。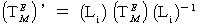
これを計算すると、次のようになります。
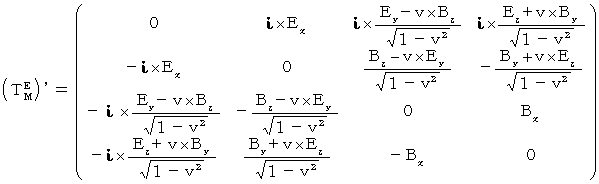
したがって、次のようになります。
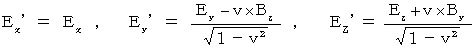
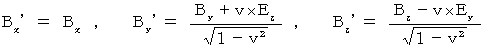
これらの式たちは、 マックスウェルの方程式を不変にする座標変換 ( ローレンツ変換 ) を導き出すときに導かれるものです。「 複素数電磁場テンソル 」は、 マックスウェル方程式を内包しています。 これが、「 複素数ローレンツ座標変換テンソル 」によって、 整合性のある座標変換を受けるのです。「 複素数ローレンツ座標変換テンソル 」は、「 複素数電磁場テンソル 」が整合性のある座標変換を受けるようにと「 ローレンツ変換テンソル 」を実数の世界から複素数の世界へと拡張して作られたものです。
複素数ローレンツ座標変換は、 直交直線座標から斜交直線座標へのベクトルの座標変換だと思いきや、 後述するように、 直交直線座標から直交直線座標へのベクトルの座標変換です。 今後は、 考えやすくするために、 1次元空間
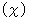 と1次元虚数時間
と1次元虚数時間 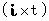 からなる2次元時空間を用いることにします。 すると、 複素数ローレンツ座標変換テンソル
からなる2次元時空間を用いることにします。 すると、 複素数ローレンツ座標変換テンソル 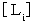 の表現行列は次のようになります。
の表現行列は次のようになります。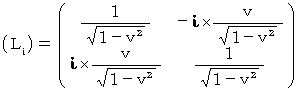
複素数ローレンツ座標変換テンソル
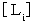 は、「 座標変換テンソル 」です。 そして、 次のような座標変換を担います。
は、「 座標変換テンソル 」です。 そして、 次のような座標変換を担います。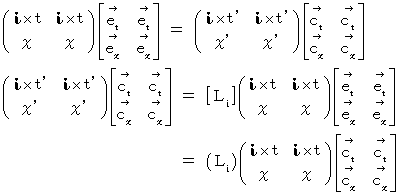
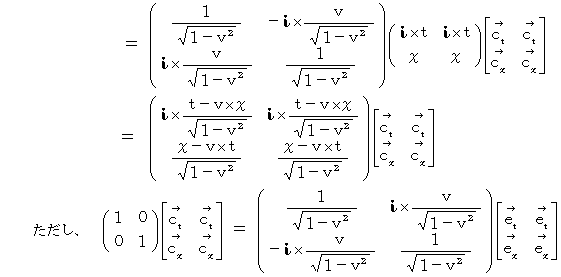
「 複素数ローレンツ座標変換テンソル 」の表現行列は、 ユニタリー行列です。 なぜなら、 次のように、 その表現行列とその転置複素共役行列の積が単位行列になるからです。
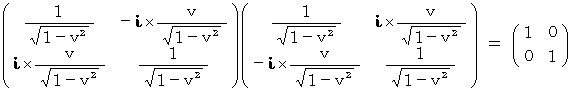
「 複素数ローレンツ座標変換テンソル 」の表現行列の行列式は
 です。
です。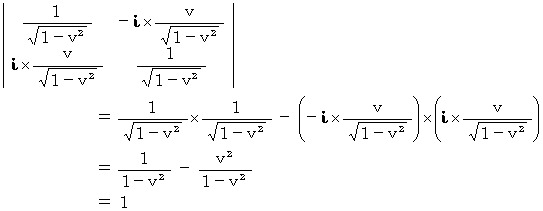
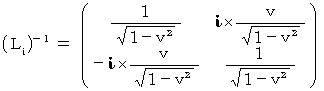 より、 座標変換後のベクトル時空間を生成する基底の標準基底表示は次のようになることがわかります。
より、 座標変換後のベクトル時空間を生成する基底の標準基底表示は次のようになることがわかります。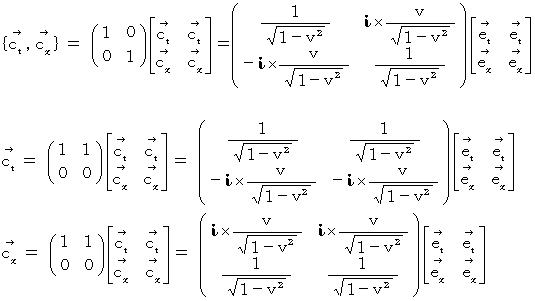
基底の要素の大きさは、 次のようになります。
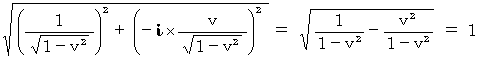
また、 基底の要素たちの内積
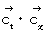 は、 次のようになります。
は、 次のようになります。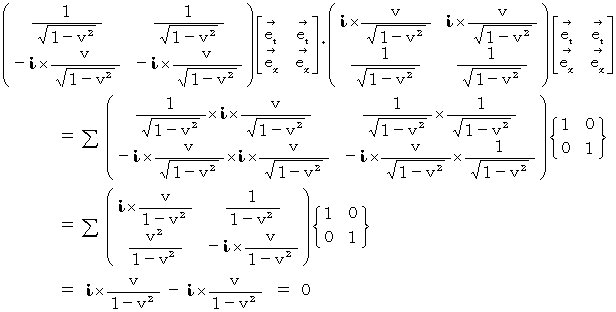
したがって、 座標変換後のベクトル時空間の計量テンソルの表現行列は次のようになります。
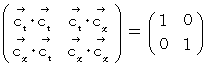
したがって、 複素数ローレンツ座標変換は、 2つの「 基底の大きさが等しい直交ベクトル空間 」の間での「 ベクトルの座標変換 」です。 ということは、 複素数ローレンツ座標変換は、 同一ベクトル空間での「 合同変換 」に置き換えることができます。
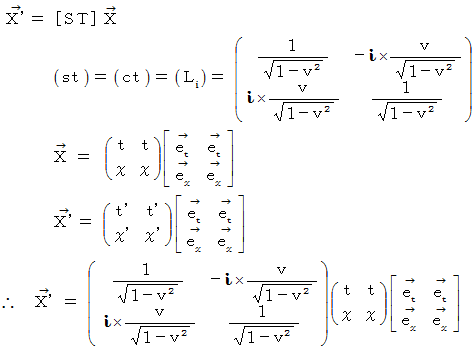
さらに、 複素数ローレンツ座標変換は、 合同変換の中でも「 回転 」に置き換えることができることについて説明します。。
一般的に、 直交座標系を反時計回りに
 回転させた新しい座標系へのベクトルの座標変換は、 次のようになります。
回転させた新しい座標系へのベクトルの座標変換は、 次のようになります。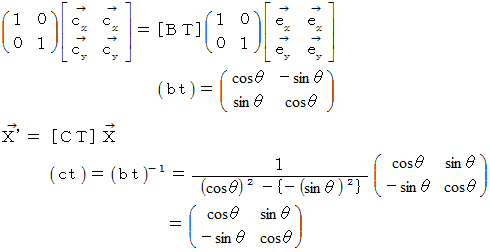
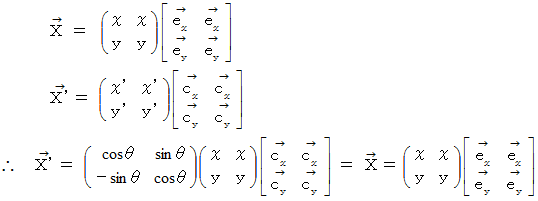
この座標変換は、 次のような時計回りの回転を表す「 演算テンソル 」による写像と同等に取り扱うことができます。
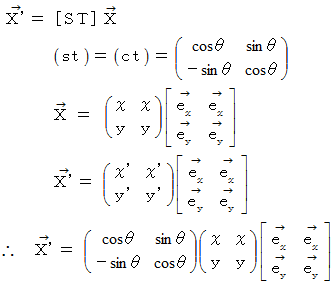
この式は、 次のように書くこともできます。
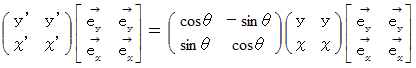
複素数ローレンツ座標変換を、 こういう形に持っていくことができるのです。 まず、 複素数ローレンツ座標変換式の行列の部分を正確に書くと、 次のようになります。
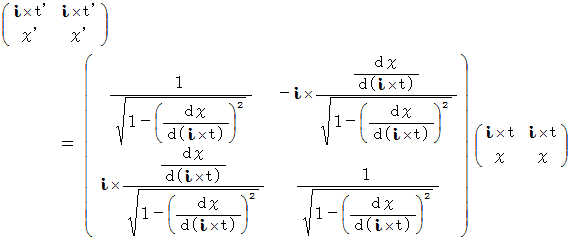
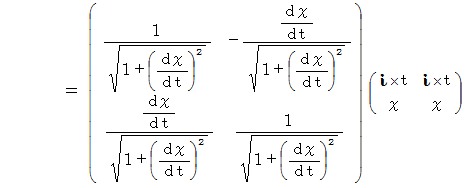
したがって、 複素数ローレンツ座標変換式は、 次のようになります。
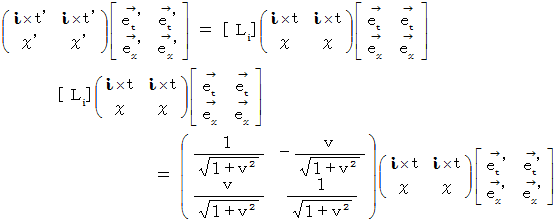
ここで、 座標変換前の基底の要素
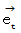 と 座標変換後の基底の要素
と 座標変換後の基底の要素 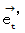 とのなす角や、 座標変換前の基底の要素
とのなす角や、 座標変換前の基底の要素 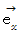 と 座標変換後の基底の要素
と 座標変換後の基底の要素 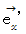 とのなす角を、 虚数角
とのなす角を、 虚数角 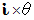 で表します。
で表します。すると、
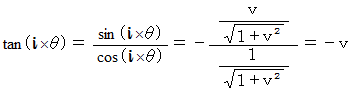
* コメント : なぜ
 にマイナスがついているのか?
にマイナスがついているのか?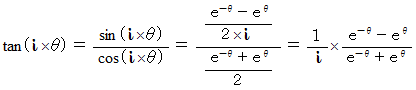 と
と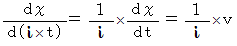 により、
により、  が
が 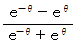
に相当することになりますが、
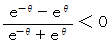 なので、
なので、  の符号
の符号をマイナスにとって、
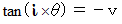 になるわけです。
になるわけです。ですので、 複素数ローレンツ座標変換式の表現行列は、 さらに次のように変形されます。
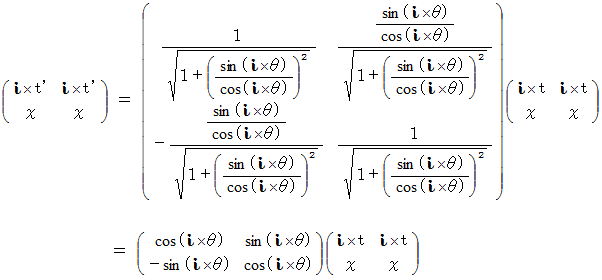
したがって、 結局、 複素数ローレンツ座標変換式は、 次のようになります。
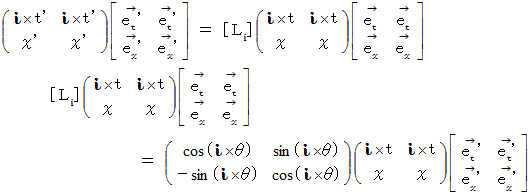
さて、
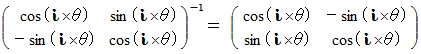 ですから、
ですから、複素数ローレンツ座標変換における基底の変換は次のように表されます。
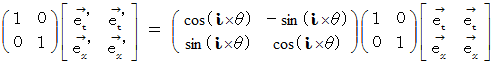
したがって、 複素数ローレンツ座標変換は、
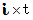 軸 を縦軸に、 x 軸 を横軸にすると、 基底の要素たちを
軸 を縦軸に、 x 軸 を横軸にすると、 基底の要素たちを 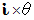 だけ時計回りに回転させることがわかります。
だけ時計回りに回転させることがわかります。複素数ローレンツ座標変換は、 直交直線座標系から直交直線座標系への変換であり、 かつ、 ベクトルの大きさを変えませんので、 次のような、 直交ベクトル空間の中での写像と同等になります。
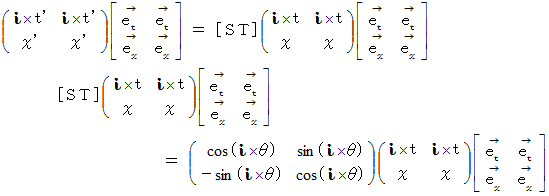
この写像は、 等長変換で、
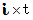 軸 を縦軸に、 x 軸 を横軸にしたときに、 ベクトルを反時計回りに
軸 を縦軸に、 x 軸 を横軸にしたときに、 ベクトルを反時計回りに 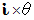 だけ回転させるものになっています。
だけ回転させるものになっています。上の式は、 次のようにも書くことができます。
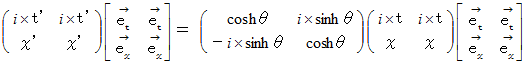
このように「 回転 」という「 合同変換 」に置き換えることのできるのは、「 複素数ローレンツ座標変換 」であって、 ローレンツ変換ではありません。 つまり、「 ローレンツ変換テンソル 」を次のような「 演算テンソル 」として取り扱うのは間違いです。
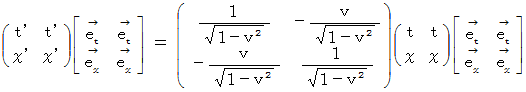
以上のことから、 実数時間の世界でのマックスウェル方程式において相対性原理が保たれるようにと導かれたローレンツ変換よりも、 虚数時間の世界でのマックスウェル方程式において相対性原理が保たれるようにと導かれた複素数ローレンツ座標変換のほうが優れていることがわかります。 そして、 このことから推測しますと、 時間を完全に虚数とする表現を用いて最初から相対性理論を記述し直せば、 相対性理論はもっと簡単で誤解されにくいものになるのではないかということです。 しかし、 私のように、 虚数時間を容認しようとしない者は、 今日の相対性理論を修正すべきであると考えています。
 論文の最初へ戻る
論文の最初へ戻る