(1) 天体測量法のしくみ ( レーザー測定法が開発される以前について )
 三角測量法 ( 点
三角測量法 ( 点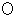 側から、 点
側から、 点 までの距離 を求める方法 )
までの距離 を求める方法 )線分
 になるべく垂直になるように、 点
になるべく垂直になるように、 点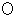 を中点とする長さ
を中点とする長さ 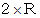 の線分
の線分  を引き、 そのそれぞれの両端と点
を引き、 そのそれぞれの両端と点  とを結ぶ2つの線分の、 線分
とを結ぶ2つの線分の、 線分  との交わる角度 ( 鋭角 ) を測定します。 両端で測定した角度の値が等しくなるように、 線分
との交わる角度 ( 鋭角 ) を測定します。 両端で測定した角度の値が等しくなるように、 線分  をわずかに回転させて調節します。 そしてその角度を
をわずかに回転させて調節します。 そしてその角度を  とします。 すると、 点
とします。 すると、 点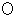 から 点
から 点 までの距離
までの距離 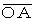 は、 次の式で与えられます。
は、 次の式で与えられます。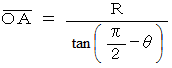
 視直径法 ( 球の直径を求める方法 )
視直径法 ( 球の直径を求める方法 )球までの距離が明らかになっていることが前提です。 それを
 メートル とします。 顔から
メートル とします。 顔から  メートル 離した物差しで見かけの球の直径を測定したら、 その値に
メートル 離した物差しで見かけの球の直径を測定したら、 その値に  をかけると、 その球の直径になります。
をかけると、 その球の直径になります。 子分の惑星から親分の星の質量を求める方法
子分の惑星から親分の星の質量を求める方法質量
 の物質が、 角速度
の物質が、 角速度  で半径
で半径  の等速円運動をしているときに、 円の中心に向かって働いている向心力
の等速円運動をしているときに、 円の中心に向かって働いている向心力  は、次のように表されます。
は、次のように表されます。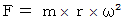
一方、 万有引力の法則は、 次のように表されます。
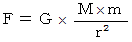
2つの式から、 次のようになります。
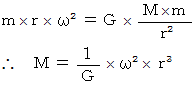
 ケプラーの第3法則 ( 子分の惑星の親分の星からの距離を求める方法 )
ケプラーの第3法則 ( 子分の惑星の親分の星からの距離を求める方法 )惑星の公転周期の2乗は、 軌道の長半径の3乗に比例します。
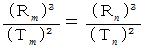
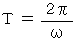 ですから、 上の式は次のようになります。
ですから、 上の式は次のようになります。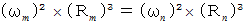
子分の惑星から親分の星の質量を求める式は次のように表されます。

したがって、 ケプラーの第3法則は次のようにも書くことができます。
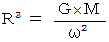
 コメント :
コメント :私たちは、 太陽のまわりを地球が公転していると言いますが、 これは、 地球の質量が太陽の質量に対して極端に小さいために、 2つの質量を加えたものは太陽の質量に等しいと見なしており、 また、 太陽の質量に対する地球の質量の比率は0であると見なしているためです。 正確には、 お互いが重心のまわりを回り合っているのです。 これは2人の共同作業です。 地球と太陽との重心とは、 言うならば、 2つを棒の両端に串刺しにして一様な重力場の中で、 吊り合うときの支点の位置です。 力のモーメントの吊り合いにより、 重心からの距離に質量をかけたものは同じ値になっています。 そして、 ケプラーの第3法則の、 厳密な式は、 次のようになります。
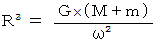
 地球の質量を求める方法
地球の質量を求める方法地球の地上での万有引力の法則は、 次のように表されます。
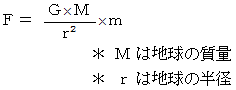
地球の地上での重力についての運動方程式は、 次のように表されます。
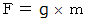
したがって、 次の式が成り立ちます。
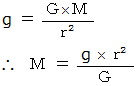
具体的な数値を代入して、
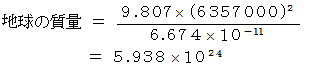
 万有引力定数
万有引力定数 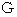 を求める方法
を求める方法1798年、 キャヴェンディッシュの鉛球実験が最初でした。 これは、 地上で2つの鉛球に作用する微小な引力を測定するものでした。 現在も、 この実験の応用で正確な
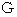 の値が測定されています。
の値が測定されています。 地球の円周を 40000 km であると定義して、 1 m の物差しを作る方法
地球の円周を 40000 km であると定義して、 1 m の物差しを作る方法円周の定義から、 地球の半径
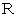 は、 次のようになります。
は、 次のようになります。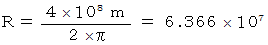
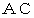 と
と 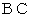 は実測できます。 そのとき、 測量には、 適当に作成した
は実測できます。 そのとき、 測量には、 適当に作成した 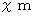 物差しを用います。
物差しを用います。すると、 次のような結果であったとします。
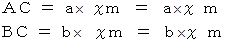
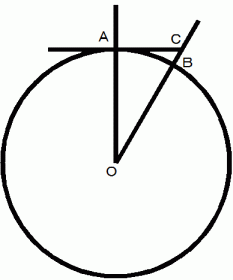
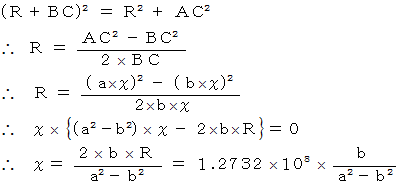
したがって、
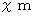 物差しの
物差しの 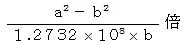 の長さの物差しが 1 m 物差しになります。
の長さの物差しが 1 m 物差しになります。 世界で初めて地球の円周を見積もった男
世界で初めて地球の円周を見積もった男ヘレニズム時代の紀元前200年ころ、 エラトステネスは、 緯度によって ( 当時は緯度という概念はないが ) 太陽の南中高度が異なることから、 地球は球であることを確認し、 その円周の大きさを計算しています。 例えば、 ある場所とその真北に位置するもう一つの場所の、 同じ日の太陽の南中高度が1度異なっており、 2つの場所の距離が
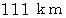 であったとしましょう。 これから地球の円周は次のようにして求めることができます。
であったとしましょう。 これから地球の円周は次のようにして求めることができます。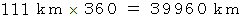
 天文学と物理学 へ戻る
天文学と物理学 へ戻る