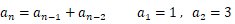
フィボナッチ数列の第２項を 1 から 3 に変えたのが リュカ数列 です。
リュカ数列の第ｎ項の値を求めましょう。

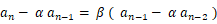　の形に持って行きたいので、
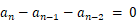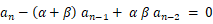　と　　を比べて、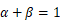
　　　
　　　
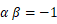
すると、 α と β は　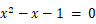 （特定方程式というやつです）の解になるので、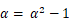
　　　
　　　


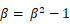
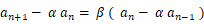
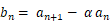　と置くと、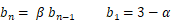
　　　
よって、
　　　
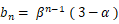
これから、先ほど導き出した４つの式のいくつかを用いてこの式を変形していきます。
　　　
　　　
　　　
　　　
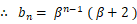
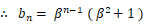
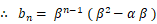
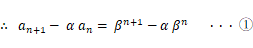
また、 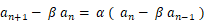　が成り立ちます。そして、同様にして次の式を導くことがでます。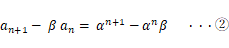
　　　
�A から �@ を辺々引いて、
　　　
　　　
　　　
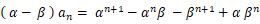
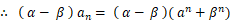
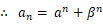
解の公式より、
　　　
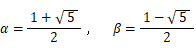
よって、
　　　

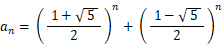
というわけで、フィボナッチ数列の第ｎ項の式によく似ていてさらにシンプルになっています。