空間の中の１つ１つの点に、 ある物理量の値としてのスカラーやベクトルが与えられているときに、「 場が形成されている 」という表現をします。 例えば、 温度や水流などです。 私は、 これらについては、「 場 」という表現よりも「 物理量空間 」という表現の方がいいのではなかろうかと考えています。 つまり、 温度は「 物理量スカラー空間 」を形成しており、 水流は「 物理量ベクトル空間 」を形成しているという言い方です。
　 一方、 空間の中の１つ１つの点に、 演算子が与えられているときを、「 場 」というべきではないかと私は考えています。 たとえば、「 重力場 」という物理量があり、 それは「 物理量ベクトル空間 」を形成しています。 しかし、「 重力場 」は、 質量というスカラーに作用して、「 重力 」という力を取り出す演算子でもあり、 物理量として取り扱われるよりも演算子として取り扱われることのほうが圧倒的に多いのです。 また、「 磁場 」という物理量があり、 それは「 物理量ベクトル空間 」を形成しています。 しかし、「 磁場 」は、 電流というベクトルに作用して、「 ローレンツ力 」という力を取り出す演算子でもあり、 物理量として取り扱われるよりも演算子として取り扱われることのほうが圧倒的に多いのです。 このように演算子的な要素の強い「 物理量ベクトル空間 」を「 場 」と呼ぶのがいいのではないかと考えます。 たとえば、 お化け屋敷なんかも、 私たちの自律神経に作用する「 霊場 」という演算子 がぎっしりと詰まった空間ですよね。

　 さて、 今日は、 重力場における「 高さ 」という概念の本質に迫ってみたいと思います。
　 ３次元空間に原点と点Ａを描いてください。 そして、 点Ａ を起点とするベクトル 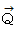を思い浮かべてください。 ただし、 ベクトル 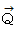には、 次の２つの条件が付いています。
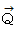　　　ベクトル の向きは、 点Ａ の位置ベクトル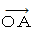（ ）と反対向きです。
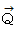　　　　ベクトル の大きさは、 点Ａ の原点から距離（ 点Ａ の位置ベクトルの大きさ ）
　　　　を 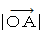としたときに、 次の式で与えられます。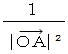
　　　　　　　
　　　　したがって、 ベクトル 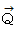の大きさは、 点Ａ の原点からの距離が大きいほど、 小さく
　　　なります。

　　　　　　　　コメント ：　球の表面積は、 中心からの距離（ 球の半径 ）の２乗に比例し、
　　　　　　　　　 　　　　次の式で与えられます。
　　　　　　　　　　　　　　　　　　

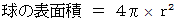
　 点Ａ 以外の すべての点にも ベクトル 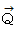と同様の性質を持ったベクトルが存在しているとします。

　 質量が 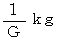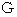（ は重力定数 ）の物質が存在する時、 空間には、 その物質による重力場が形成されており、 それは、 上記の ベクトル 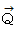で表されます。
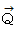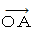ベクトル を　　と　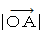 を用いて表すと、 次のようになります。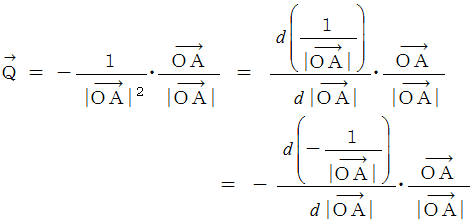
　　　　　
　　　　　

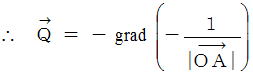
すると、 ベクトル解析学の公式より、 次のことが言えます。
　　　　　　スカラー場 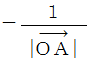の勾配は、 ベクトル　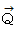である。

　　　　　　　　　　　　　　コメント ：　スカラー場 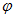の勾配は、 次の式で表されます。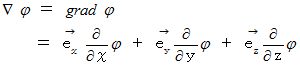
　　　　　　　　　　　　　　　　　　　　　　

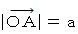　 さて、 ベクトル の大きさは、 その点に存在する質量 １ｋｇ の物質を重力に抗して移動させるときに必要な力の大きさに等しいので、 質量 １ｋｇ の物質をベクトル の方向に、 から 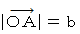まで移動させたときの仕事は、 次の式のようになります。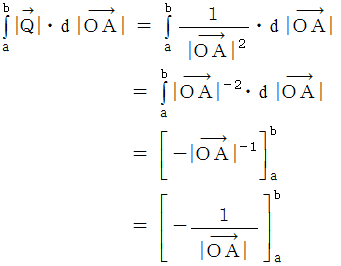
　　　　　
　 この 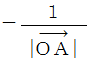　と　勾配ベクトル 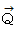を生みだすスカラー場 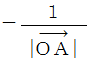が等しいと言うことは、 スカラー場 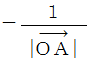は、 質量 １ｋｇ の物質の位置エネルギー分布を表していると言うことができます。 したがって、 ベクトル解析学では、 次のような言い方で表します。
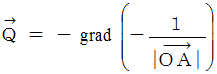　　　　　のとき、
　　　　　　　　スカラー場 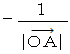は、 ベクトル場 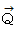のポテンシャルである。

　 ポテンシャル 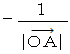は、「 質量 １ｋｇ の物質の位置エネルギーの絶対値（ ただし、 エネルギー水準を 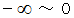とする ）」であり、 私はこれを、「 電位 」に対応させて、「 重位 」と言っています。 ちなみに、 電位の差は「 電圧 」ですから、「 重位 」の差が「 重圧 」です。 今まで述べたのは、 質量が 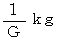の物質が作り出す重力場についてですので、 一般的には、 質量が 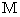ｋｇ の物質が作り出す重力場については、「 重位 」は 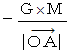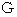（ は重力定数 ）になります。

　 「 重位 」 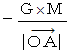は、「 質量 １ｋｇ の物質の位置エネルギーの絶対値（ ただし、 エネルギー水準を 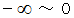とする ）」です。 また、「 重圧 」は、「 重位差 」のことであり、「 重位の低い所から重位の高い所に 質量 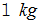の物質を移動させるのに必要な仕事 」で表されます。（ 重力場を作り出している物質に近いほど、 重位は小さくなっています。 重位は負の数です。）また、「 重位 」の勾配にマイナス１ をかけたものは、 重力場です。