勾配とは、 方向を持った傾きのことであり、 ｚ 軸に平行な一様な重力場が存在する３次元空間の中の曲面上の１点に小さなボールを置いたときに、 そのボールがどんな加速度（ 加速度は大きさと方向をもった量です。）で転がるかを表したようなもの（ 加速度そのものの大きさではありませんが ・ ・ ・ ）です。 その状況を、 x y 平面を真上から眺めたニ次元平面上の各点に、 ボールの加速度の、 方向は投影し大きさに比例するように対応させた二次元ベクトルで表すと、 簡単な図で表すことができます。 x y 平面上のすべての点で、 その点を起点とする勾配ベクトルが存在するのですが、 それをすべて表現することはできませんので、 整数だけの成分からなる x y 平面上の点のみについてだけ勾配ベクトルを表記することにします。 こうしてできたのが、 勾配ベクトルマップです。
　 しかし、 この勾配マップよりも、 はるかに簡単に作ることができて、 もっと勾配をイメージしやすいマップがあります。 それは、 等高線マップです。 曲面上の ｚ 座標値が等しい点を結んで、 x y 平面に投影したものです。 勾配ベクトルは、 等高線に垂直で、 等高線と等高線の間が狭いほど大きいですので、 等高線マップから、 x y 平面上の各点を起点とする勾配ベクトルをイメージすることが可能です。

　 以上の等高線マップは、 一様な重力場における３次元空間の２次元的表現でしたが、 今度は、 等高線マップを、 一般的な重力場における３次元空間の３次元的表現に拡張してみましょう。「 等高線 」は「 等高面 」になります。 正確には「 等位面 」と言います。「 等位面 」とは、 ポテンシャルの等しい面のことを言います。
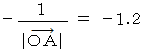　　　　になる点の集まりは、 半径 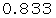の球面になり、
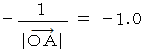　　　　になる点の集まりは、 半径 の球面になり、
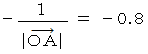　　　　になる点の集まりは、 半径 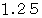の球面になり、
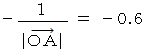　　　　になる点の集まりは、 半径 の球面になります。

　 これらの球面を、 ３次元グラフで表すと、 原点を中心として、 次第に間隔が広がっていく４つの球面になります。 この３次元等位面マップからイメージできる勾配ベクトルは、 ベクトル 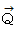に一致します。 ただし、 原点は無限大の頂上ではなくて、 無限大の深みです。 なんだかブラックホールのようです。、 原点から無限大に離れている所の高さが で、 それから次第に原点に近づくにつれて、 深くなっていきます。 等位面間隔が一定であるときは、 勾配は一定であり、 勾配ベクトルの大きさは一定ですが、 この勾配ベクトル空間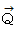 では、 原点に近づくにつれて勾配が急になって、 勾配ベクトルの大きさは大きくなってきます。


　 マクロ的に見た時に、 この辺りならば、 重力場は一様であると考えて差し支えないということがあります。 一様な重力場とは、 空間のどんな点をとってもそれを起点とする重力場を表すベクトルの大きさと向きが同じであるということです。 「 重位 」の勾配に −１ をかけたものが重力場であり、「 重位 」の等しい面が「 等位面 」ですから、 一様な重力場、 つまり 一様な「 重位 」の勾配、 の条件下では、 等位面の間隔は一定です。 一様な重力場における 等間隔の「 等位面 」のことを「 等高面 」と言います。 等高線マップは、 曲面 と 等高面 の接線 の x y 平面への投影です。

　　　一様な重力場では、「 重圧 」は、「 垂直方向への距離 」に比例します。
　　　一様な重力場では、「 重圧 」＝ −「 重力場 」×「 垂直方向への距離 」　です。
　　　一様な重力場では、「 重力場 」＝ −「 重圧 」÷「 垂直方向への距離 」　です。
　　　一様な重力場では、「 垂直方向への距離 」＝ −「 重圧 」÷「 重力場 」　です。

　 垂直線上での重位の目盛りの間隔からは「 重位 」の勾配にマイナス１ をかけたもの、 つまり、「 重力場 」をイメージすることができます。 しかし、 私たちが等高線マップからイメージするのは、「 重力場 」ではなく、「 傾斜（ 傾き ）」です。 つまり、 水平線と垂直線からなる２次元平面における、 水平線と垂直線を結ぶ線分の傾きです。 傾きは勾配ではありません。 また、 傾きは高さでもありません。 高さとは、 一様な重力場における、 垂直線の長さ、 つまり垂直方向への距離、 です。

　 たとえば、 地球の地表は一様な重力場とみなされ、 その重力場の大きさが、 重力加速度 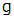です。 海抜 ０ ｍ から 海抜 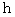メートル の高さに 質量 １ｋｇ の物質を持ち上げた場合は、 その物質の位置エネルギーの差は 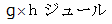になります。 質量 １Ｋｇ の物質における位置エネルギーの差は、「 重圧 」です。 一様な重力場では、「 重圧 」＝ −「 重力場 」×「 垂直方向への距離 」　です。

　 地球の地表近くでは、「 重位（ 重力場のスカラーポテンシャル ）」は次のように表されます。
　　　　

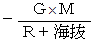
海抜 ０ ｍ と 海抜 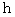メートル の「 重圧 」は、 次のようになります。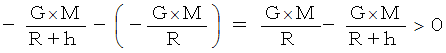
　　　　
　　　　　　　　　　重位は負の数で、 重力を作り出す物質の中心に近い所ほど小さいです。
これをもっと簡単な式にしてみましょう。
　　　
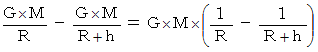
　　　　　　ここで、 テーラー展開により、 次の式が成り立ちます。
　　　　　　　　　
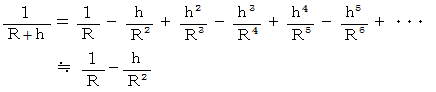
　　　　　　よって、次の式が成り立ちます。
　　　　　　　　　

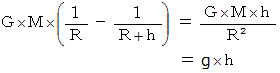
　 以上より、「 重圧 」は、「 質量 １ｋｇ の物質の位置エネルギーの差 」、 つまり「 重位の差 」、 であることに間違いはないことがわかりました。


　 以上の考察の結果から、 高さの本質が明らかになります。 高さとは「 重位 」ではありません。 重位とは、 質量 １ｋｇ の物質の持つ絶対的位置エネルギーのことです。 また、 高さとは「 重圧 」でもありません。 重圧とは重位の差のことです。 また、 高さとは「 重力場を作り出している物質の中心からの距離 」でも「重力場を作っている物質の中心からの２つの距離の差」でもありません。 高さとは、 一様な重力場において、 重力場の方向と逆向きの数直線上の２点の、 小さい点から大きい点への位置ベクトルの大きさです。 高さとは、 一様な重力場において、「 重圧 」を「 重力場 」で割ったものにマイナス１ をかけたものです。「 重力場 」とは「 重位 」の勾配にマイナス１ をかけたものですから、 高さとは、 一様な重力場において、「 重位の差 」を「 重位の勾配 」で割ったものです。