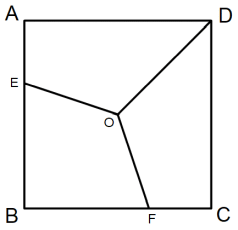
ＯＡ ＝ ОＢ ＝ ОＣ ＝　ОＤ
　　　　　　　　ＡＤ ＝ ＣＤ ＝ ３
　　　　　　　　ＡＥ ＝ ＣＦ ＝ １
　　　　　　　　ＢＥ ＝ ＢＦ ＝ ２

　正方形を等しい面積に３分割する方法に、正方形の中心 と 頂点Ｄ とを結ぶ線分で切断し、かつ、正方形の中心 と 辺ＡＢを 1:2 に内分する点 とを結ぶ線分で切断し、かつ、 正方形の中心 と 辺ＢＣを 2:1 に内分する点 とを結ぶ線分で切断する というのがあります。その理由を考えてみましょう。

　　　　

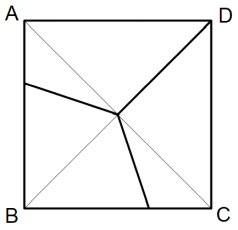
　補助線ＡＣとＢＤを加えると正方形は６つの三角形に分割されます。これらを正方形の辺になる部分を底辺とする三角形たちとみなすと、高さがすべて等しくなっています。ということは、三角形の面積は底辺の長さに比例するということになります。

　というわけで、あとは見てのとおりで、正方形は等しい面積に３分割されていることが分かります。