（１） 次の図の証明をしなさい。

　　　　　
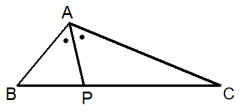
　　　　　　　　　　　ＢＰ ： ＣＰ　＝　ＡＢ ： ＡＣ

　 解 答 ：

　　　　　

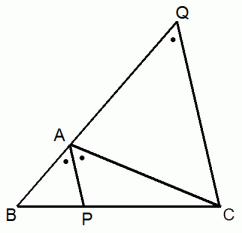
　　線分ＢＡを延長してＢＱを作る。 ただし、 ＡＱ ＝ ＡＣ とする。
　　△ＡＣＱは二等辺三角形なので、 ∠ＡＣＱ ＝ ∠ＡＱＣ
　　∠ＣＡＱ　＝　１８０°− ２×∠ＡＱＣ
　　∠ＣＡＱ　＝　１８０°− ２×∠ＢＡＰ
　　したがって、 ∠ＡＱＣ ＝ ∠ＢＡＰ
　　したがって、 ＡＰ と ＱＣ は平行
　　したがって、 ∠ＡＰＢ ＝ ∠ＱＣＢ
　　したがって、 △ＡＢＰ と △ＱＢＣ は相似
　　したがって、 ＡＢ ： ＱＢ　＝　ＢＰ ： ＢＣ
　　したがって、 ＡＢ ： ＱＡ　＝　ＢＰ ： ＣＰ
　　したがって、 ＡＢ ： ＡＣ　＝　ＢＰ ： ＣＰ
　　　　　　　　　　　　　　　　　　（ 証明終わり ）

（２）
　　　　　

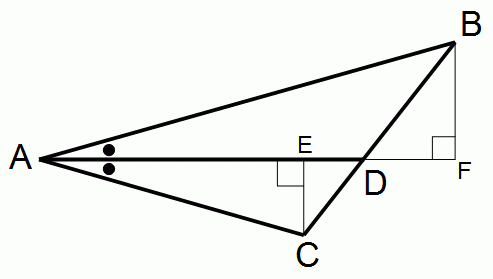
三角形ＡＢＣがあります。 角Ａの二等分線と辺ＢＣとの交点をＤとします。
ＡＢ ： ＡＣ　＝　ＢＤ ： ＣＤ　であることを証明しなさい。
ヒントは図に示しています。

　 解 答 ：

△ＡＢＦ と △ＡＣＥ は相似です。
　　　したがって、 ＡＢ ： ＡＣ　＝　ＢＦ ： ＣＥ　　　　・ ・ ・ ・
△ＢＦＤ と △ＣＥＡ は相似です。
　　　したがって、 ＢＤ ： ＣＤ　＝　ＢＦ ： ＣＥ　　　　・ ・ ・ ・

と より、
　　　 ＡＢ ： ＡＣ　＝　ＢＤ ： ＣＤ