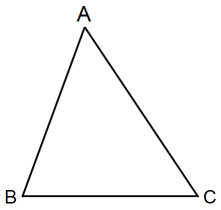
「 △ABCを面積比が １：２ になるように２分しなさい。」と言われたら、辺BCを １：２ に内分する点と頂点Aを結べばいいのですが、「 辺BCに平行な線分で２分しなさい。」という条件がつくと難しくなります。△ABCの高さを h とすると、h を上から １：何？ に内分する点を通る線分になるでしょうか？

　　　　　　　

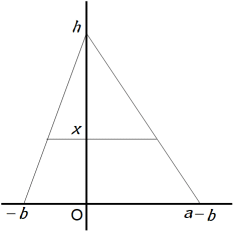
　底辺BCよりも x 上方の底辺BCに平行な線分が△ABCを面積比 １：２ に２分するものとします。そして、底辺BCの長さを a とします。すると、２つの三角形の面積比から次の式が成り立ちます。
　　　
　　　
　　　
　　　
　　　
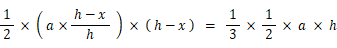
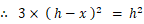
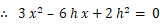
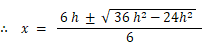
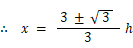
　0 ＜ x ＜ h より、
　　　
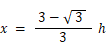
　したがって、高さ h を上から次の比に内分する点を通る底辺に平行な線分が、△ABCを面積比 １：２ に２分するものになります。
　　　
　　　
　　　

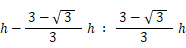
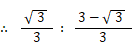
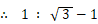
　ちなみに、高さ h を上から ２：１ の比に２分する点を通る底辺に平行な線分は三角形の重心を通ります。