(1) 辺の長さ や 角の角度 から求める方法
-
2辺の長さとその2辺がなす角が決まれば、 三角形が決まります。 つまり、 2辺の長さとその2辺がなす角が等しくて、 形または大きさが異なる三角形はありません。
2辺の長さと1つの角が等しくて、 形または大きさが異なる三角形たちがあります。 たとえば、 次の図の
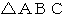 と
と 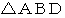 です。
です。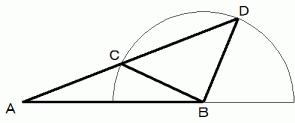 。
。3つの角がそれぞれ等しくて、 大きさの異なる三角形たちは無数にありますが、 3辺の長さがそれぞれ等しくて、 形または大きさが異なる三角形はありません。
ということは、 三角形の面積の公式は、
 だけではなく、 他に少なくとも2つあるということです。 1つは、 2辺の長さとその2辺がなす角が要素になっているものであり、 もう1つは3辺の長さが要素になっているものです。
だけではなく、 他に少なくとも2つあるということです。 1つは、 2辺の長さとその2辺がなす角が要素になっているものであり、 もう1つは3辺の長さが要素になっているものです。( 前者の証明 )
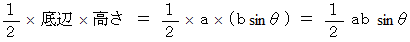
( 後者の証明 )
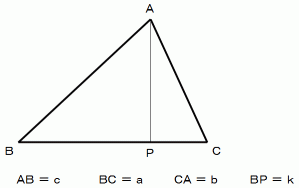
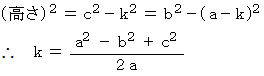
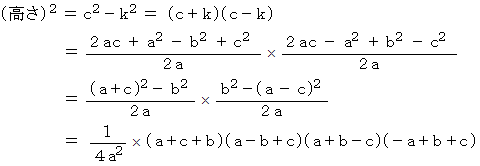
ここで、
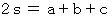 とおくと、
とおくと、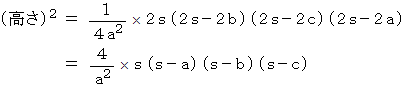
したがって、
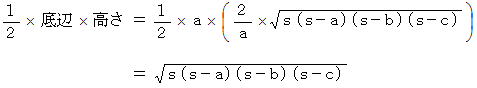
-
原点
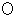 と
と 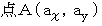 と
と 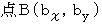 を結んでできる三角形の面積は次の式で求めることができます。
を結んでできる三角形の面積は次の式で求めることができます。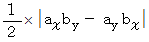
( 証明 )
内積の定理より、
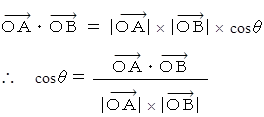
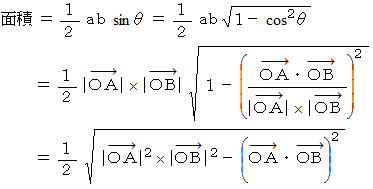
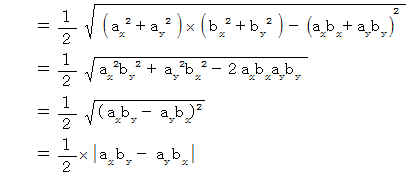
上記の式の途中で出てきた次の式は、 位置ベクトルの内積を用いて三角形の面積を求めるものです。 覚えておくと便利です。
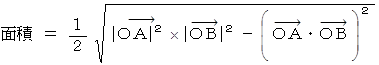
 その他の数学 へ戻る
その他の数学 へ戻る