【 問 題 】
-
△ABC がある。
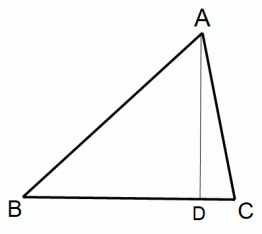
辺ACの長さ = b
辺ABの長さ = yb
辺BCの長さ = xb
ただし、
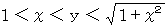
(1) 角Aから辺BCに対して下した垂線の交点をDとするとき、 CDの長さを求めよ。
(2) CDの長さはBCの長さの半分未満であることを証明せよ。
-
CDの長さを Q とし、 ADの長さを L とすると、 ピタゴラスの定理より、
( yb )2 = L2 + ( xb − Q )2
つまり、
y2b2 = L2 + x2b2 − 2xQb + Q2 ・ ・ ・

b2 = L2 + Q2 ・ ・ ・

 から
から  を辺々引いて、
を辺々引いて、( y2 − 1 ) b2 = x2b2 − 2xQb
よって、
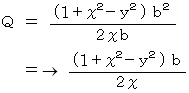
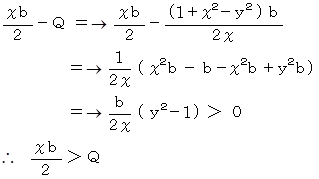
 幾何学 へ戻る
幾何学 へ戻る