（ 問 題 ）

　　　　点Ｐを通って△ＡＢＣの面積を２等分する直線を描きなさい。
　　　　　　　　


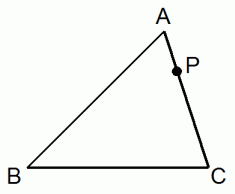
（ 解 答 ）

　　　　　　　　

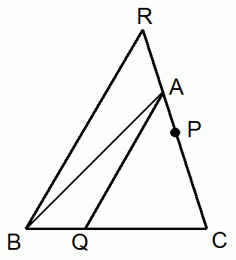
　　　　線分ＰＣ と 線分ＰＲ の長さは等しい。
　　　　線分ＲＢ と 線分ＡＱ は平行である。
　　　　点Ｐ と 点Ｑ を結ぶ直線が、 △ＡＢＣの面積を２等分する。


（ その理由 ）

　　　　　　　　

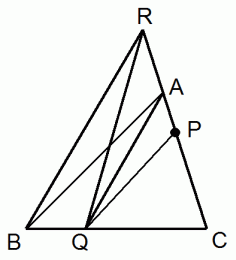
　　　　△ＡＢＱ と △ＡＲＱ の面積は等しい。
　　　　　　＊　線分ＲＢ と 線分ＡＱ は平行だから、底辺ＡＱを共有する２つの三角形の高さは等しいので
　　　　したがって、□ＡＢＱＰ と △ＰＲＱ の面積は等しい。
　　　　△ＰＲＱ と △ＰＱＣ の面積は等しい。
　　　　　　＊　線分ＰＣ と 線分ＰＲ の長さは等しいので
　　　　したがって、□ＡＢＱＰ と △ＰＱＣ の面積は等しい。